Les éléments de symétrie de la classe cubique m3m sont :
Un centre de symétrie, 3 axes d'ordre 4 de type [100], 3 miroirs M de type (100) normaux aux axes 4, 4 axes d'ordre 3 [111, 6 axes d'ordre 2 de type [110] et 6 miroirs M' de type (110) normaux aux axes d'ordre 2.
Par convention on écrit ces éléments de symétrie sous la forme :

C, 3A₄ / 3M, 4A₃, 6A₂ / 6M'.

Dans le système cubique une rangée [hkl] est toujours normale à la famille de plans réticulaires d'indices (hkl).

On peut noter quelques particularités concernant ces éléments de symétrie :
- Les axes ternaires sont les intersections de 3 miroirs de type M'.
- Quand on tourne autour d'un axe binaire (par exemple la rangée [1,−1,0]), on rencontre un axe binaire [110], un axe ternaire [111] un axe tétragonal [001] puis un autre axe ternaire [−1,−1,1].
- L'angle entre deux axes ternaires vaut 109°28'.
- L'angle entre un axe 4 et un axe 3 vaut 54°44'.

Utilisation:
Dans le programme, on considère un cube immobile placé dans le repère Oxyz. L'observateur O' se déplace autour de O et l'écran de projection est normal à la direction OO'. OO₁ est la projection de OO' sur le plan Oxy.
On utilise des coordonnées sphériques : ρ est la distance OO', φ est l'angle entre OO' et OO₁, θ est l'angle entre Ox et OO₁.
Commandes :
Des cases à cocher permettent de choisir les éléments que l'on désire visualiser.
Comme la représentation des 6 miroirs M' est trop confuse, une liste de choix permet de sélectionner le miroir à afficher. L'ordre retenu permet de voir qu'un axe ternaire est l'intersection de trois miroirs M'.
Prendre θ = 45° et φ = 35 ou 145° pour avoir un axe ternaire normal au plan de projection.

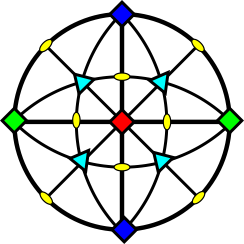Projection stéréographique des éléments de symétrie du cube (m3m)