On considère un flux de particules de masse M et d'énergie E qui arrive sur une barrière de potentiel de rectangulaire de hauteur V et de largeur a. Il y a un flux de particules réfléchies et contrairement au modèle classique, un flux de particules transmises. Ces flux sont caractérisés par des ondes progressives de type Ψ = Ψ0sin(ω.t − k.x) (avec E = ħω.)
L'équation de Schrödinger s'écrit :
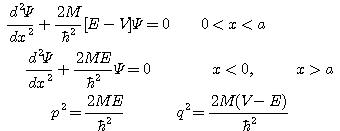
A droite de la barrière, la solution est de la forme : Ψ = A.cos(px).sin(ω.t) − A.sin(px)cos(ω.t) = Ψ1 − Ψ2 = A.sin(ω.t − p.x)
Si E < V
Pour 0< x < a, la solution est la somme Ψ3 − Ψ4 avec :
Ψ3 = [B.eqx + C.e-qx].sin(ω.t) et Ψ4 = [D.eqx + E.e-qx].cos(ω.t). La continuité de la fonction d'onde et de sa dérivée pour x = a permet de déterminer les valeurs des constantes B, C, D et E .
A gauche de la barrière la solution est la solution est la somme Ψ5 - Ψ6 avec :
Ψ5 = [F.sin(qx) + G.cos(qx)].sin(ω.t) et Ψ6 = [H.sin(qx) + K.cos(qx)].cos(ω.t).
Vérifier que c'est la somme d'une onde progressive qui se dirige vers la barrière (particules incidentes) et d'une onde progressive qui s'en éloigne (particules réfléchies). La continuité de la fonction d'onde et de sa dérivée pour x = 0 permet de déterminer les valeurs des constantes F, G, H et K.
Les vitesses des particules incidentes et transmises étant identiques, le rapport des flux transmis et incidents est égal au rapport du carré des amplitudes des fonctions d'onde. Un calcul fastidieux conduit à :
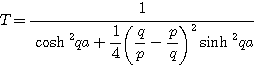
Si l'on envoie 100 particules sur la barrière, 100.T sont transmises et 100.(1 − T) sont réfléchies.
Si E > V
Pour 0< x < a, la solution est la somme Ψ3 - Ψ4 avec :
Ψ3 = (B.sin(qx) + C.cos(qx)).sin(ω.t) et Ψ4 = (D.sin(qx) + E.cos(qx)).cos(ω.t) avec cette fois : q2 = 2M(E − V) / ħ2.
La continuité de la fonction d'onde et de sa dérivée pour x = a permet de déterminer les valeurs des constantes B, C, D et E . Comme dans le cas précédent à gauche de la barrière la solution est la somme d'une onde progressive qui se dirige vers la barrière (particules incidentes) et d'une onde progressive qui s'en éloigne (particules réfléchies).
Cette fois, le rapport des flux transmis et incidents est égal à :
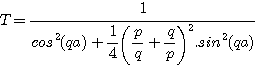
Dans la barrière, le nombre d'onde est q = 2.π / λ. On peut noter que si q.a = n.π (n entier) alors T = 1 :
Pour les valeurs λ = 2a / n, il y a résonance.
Consulter cette page pour une étude plus détaillée.
Utilisation :
Les unités sont arbitraires (2M.ħ2 = 1). La hauteur de la barrière est fixée à V = 5.
Les boutons radio permettent de visualiser l'animation ou la courbe T = f(E).
Les curseurs permettent de modifier la valeur de la largeur a de la barrière et celle de l'énergie E.
Animation
La courbe en rouge représente la fonction d'onde des particules incidentes. Celle en bleu la fonction d'onde des particules réfléchies. La courbe indigo correspond à la fonction d'onde totale dans l'espace à gauche de la barrière. La courbe en vert représente la fonction d'onde des particules transmises.
Tester pour différentes valeurs de a et de E. Examiner par exemple le cas a = 2 et E voisin de 7,45.
Courbe T = f(E)
Faire varier la valeur de la largeur de la barrière. Bien noter les oscillations de T pour de E > V pour les largeurs de la barrière supérieures à 1.
