Si l'on approche un aimant d'un solénoïde relié à un ampèremètre, on constate l'apparition d'un courant induit dans le circuit.
L'aimant crée un flux Φ dans le bobinage et son déplacement provoque une variation dΦ de ce flux.
Cette variation de flux induit une fem e dont la valeur est :
e = − dΦ / dt.
C'est la loi de Lenz.
Le courant induit s'oppose par ses effets à la cause qui lui donne naissance. Quand on approche le pôle Nord de l'aimant du solénoïde, le sens du courant induit est tel qu'il crée une face Nord sur la partie supérieure du bobinage.
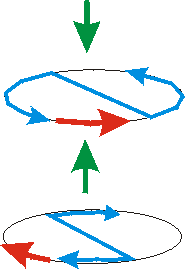
Pour retrouver le sens du courant, on peut utiliser le moyen mnémotechnique suivant : En joignant deux flèches (ayant le sens du courant), opposées sur la spire, on dessine un N.
Si on éloigne le pôle Nord de l'aimant ou si l'on approche un pôle sud, le sens du courant induit est inversé. En utilisant la méthode précédente, on dessine cette fois un S.
Comme l'intensité du courant est fonction de la dérivée du flux par rapport au temps, elle est fonction de la vitesse de déplacement de l'aimant.
Pour donner une allure réaliste à cette simulation, j'ai modélisé l'aimant par un doublet magnétique (deux masses magnétiques +m et -m distantes de L) et supposé que cet aimant se déplace à vitesse constante V le long de l'axe du solénoïde.
Par intégration sur la surface de chaque spire, on calcule le flux induit par chaque masse magnétique puis par intégration sur la hauteur du bobinage, on peut obtenir le flux total. On déduit la valeur de la fem induite par dérivation de ce flux par rapport au temps.
Utilisation :
Il est possible de modifier la vitesse (constante) de déplacement de l'aimant. La longueur et le sens de la barre rouge correspondent à l'intensité et au sens du courant. De même la flèche noire tracée sur le solénoïde représente le courant dans le circuit.