Dioptres sphériques

Les dioptres sphériques sont des systèmes centrés simples dont l'étude montre l'intérêt et les limites de l'approximation de Gauss. Ce sont des systèmes de révolution et on conduit l'étude dans un plan contenant l'axe optique. Selon la première loi de Descartes un rayon incident contenu dans ce plan est réfracté dans ce plan.

Dioptre sphérique

Un dioptre sphérique est une calotte sphérique qui sépare deux milieux transparents homogènes isotropes d'indices N₁ et N₂. Le plan contenant l'axe optique et le rayon incident forment le plan d'incidence. Le rayon réfracté est contenu dans ce plan.

Stigmatisme du dioptre sphérique

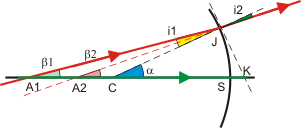Une source ponctuelle A1 émet un rayon A1C passant par le centre du dioptre. Ce rayon arrive sous incidence nulle et n'est pas dévié.. La normale au dioptre en J est CJ. Le rayon A1J arrive sur le dioptre avec l'incidence i1. Il est réfracté avec un angle de i2 tel que N1.sin i1 = N2.sin i2 Ce rayon coupe l'axe optique en A2. La partie JA2 est virtuelle.

Dans les triangles CJA1 et CJA2, on a : CA1 / sin i₁ = JA1 / sin α et CA2 / sin i₂ = JA2 / sin α .
Or N₁.sin i₁ = N₂.sin i₂
On en déduit que N₁.CA1 / JA1 = N₂.CA2 / JA2 .
La quantité N.CA / JA constitue un invariant de la réfraction.

Stigmatisme rigoureux
Il y a stigmatisme rigoureux si la position du point B ne varie pas quand J se déplace sur la surface du dioptre.

Si CA1 = 0, alors CA2 = 0 : Le dioptre est stigmatique pour son centre.
Si JA1 / JA2 est constant, il y a également stigmatisme rigoureux. Ce rapport est constant si le dioptre coïncide avec la sphère lieu des points dont le rapport des distances à deux points fixes est constant.

L'invariant N.CA / JA s'applique quand J est confondu avec S.
N₁.CA1 / SA1 = N₂.CA2 / SA2 soit N₁.CA1 / (SC + CA1) = N₂.CA2 / (SC + CA2) (a)

Si T est l'autre extrémité du diamètre CS, on a aussi SA1 / SA2 = − TA1 / TA2 et −N₁.CA1 / TA1 = N₂.CA2 / TA2.
N₁.CA1 / (TC + CA1)= N₂.CA2 / (TC + CA2) (b)
En combinant les relations (a) et (b), on tire ;

CA1 = SC.N₂ / N₁ et CA2 = SC.N₁ / N₂

Ces points conjugués rigoureusement stigmatiques sont connus sous le nom de points d'Young-Weierstrass.
Un des points est virtuel et l'autre réel. Ils sont situés tous les deux du même côté du centre de la sphère.

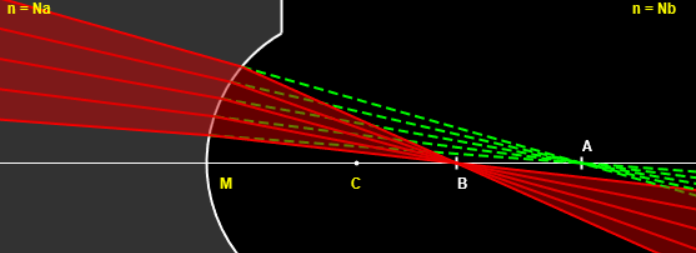
Stigmatisme approché
Il y aura stigmatisme approché si J est voisin du sommet (conditions de Gauss).

On pose d = JS i1 = β1 − α = − d / SA1 + d / SC i2 = β2 − α = − d / SA2 + d / SC Or N1.i1 = N2.i2 N1(1 / SC − 1 / SA1) = N2(1 / SC − 1 / SA2) Ou encore N1 / SA1 − N2 / SA2 = (N1 − N2) / SC

Exemple de situation hors des conditions de Gauss

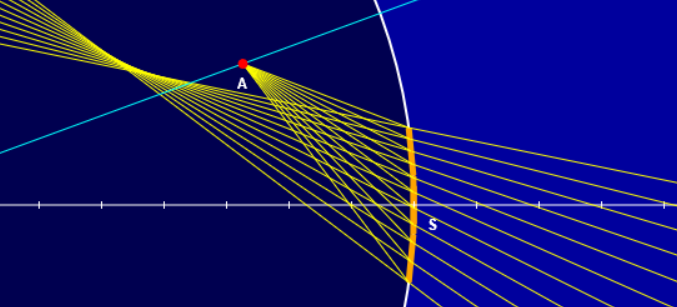
Formules de conjugaison

Cas particuliers :

⇒ SA1 = SC entraîne SA2 = SC : on retrouve le fait que le centre optique est sa propre image.

⇒ SA1 = − ∞ alors SA2 = SFi = SC.N₂ / (N₂ − N₁).

Fi est le foyer image. A un rayon incident parallèle à l'axe, correspond un rayon réfracté qui passe par Fi.

Si Fi est réel, le dioptre transforme un faisceau parallèle en un faisceau convergent qui passe par Fi : le dioptre est dit convergent

Si Fi est virtuel, le dioptre transforme un faisceau parallèle en un faisceau divergent qui passe par Fi : le dioptre est dit divergent.

⇒ SA2 = ∞ alors SA1 = SFo = SC.N₁ / (N₁ − N₂).
Fo est le foyer objet. A un rayon incident passant par Fi correspond un rayon réfracté parallèle à l'axe.

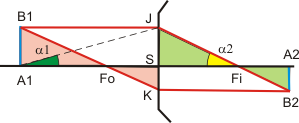On a A1B1 = SJ et A2B2 = SK La similitude des triangles A1B1Fo et FoSK donne : A1B1 / A2B2 = − SFo / FoA1 La similitude des triangles A2B2Fi et FiSJ donne : A1B1 / A2B2 = − FiA2 / SFi

En écrivant l'égalité de ces deux expressions du grandissement, on obtient la relation de conjugaison de Newton avec origines aux foyers : SFo.SFi = FoA1.FiA2 .

Relations de conjugaison du dioptre sphérique

Origine au sommet Origine au centre   Origines aux foyers

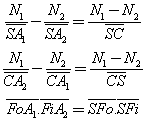Foyer objet Foyer image     Grandissement

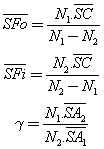Remarque :

En faisant R = ∞ on retrouve les formules du dioptre plan.
En faisant N2 = − N₁, on retrouve les formules des miroirs sphériques.

Positions des images

Construction des images.
Un objet A1B1 donne une image A2B2. Si A1 est sur l'axe optique A2 est également sur cet axe. Pour construire B2, on utilise des rayons particuliers.

* Tous les rayons passant par le centre du dioptre ne sont pas déviés.
* Tous les rayons parallèles à l'axe optique (qui correspondent à un objet à l'infini) passent par le foyer image.
* Tous les rayons issus du foyer objet émergent parallèlement à l'axe optique.

Pour les constructions, on a utilisé les deux premiers rayons.

Cas des objets à l'infini.
Si le plan objet est à l'infini, le plan image est dans le plan focal image. Pour un faisceau faisant l'angle θ avec l'axe optique, le point de convergence est situé à l'intersection du plan focal image avec le rayon passant par O, incliné de θ sur l'axe optique.

Le programme permet de choisir R positif ou négatif et N₁ > N₂ ou N₁ < N₂.
Vérifier que les quatre possibilités offertes correspondent en fait à un dioptre divergent et à un dioptre convergent (principe du retour inverse de la lumière).
Le programme permet d'étudier aussi le cas N2 = − N₁ qui correspond au miroir mais dans ce cas, l'échelle utilisée n'est pas optimale.

Un curseur de couleur cyan permet de repérer les positions des points A1 et A2 et de vérifier les formules de conjugaison.

Relation de Lagrange-Helmholtz

SJ = −SA1.tan α1 = −SA2.tan α2 Dans les conditions de Gauss, on peut écrire : SA1.α1 = SA2.α2. (a) Or A2B2 / A1B1 = N1.SA2 / N2.SA1 (grandissement) Donc N1.SA2.A1B1 = N2.SA1.A2B2 En tenant compte de la relation (a), on obtient : N1.A1B1.α1 = N2.A2B2.α2

Cette relation dite de Lagrange-Helmholtz indique que la quantité N.AB.α est un invariant pour la réfraction.

En faisant N₁ = −N₂, on obtient une relation identique pour les miroirs sphériques.