Optique géométrique

---

Postulats de l'optique géométrique

L'optique géométrique se déduit sans autre hypothèse des deux postulats suivants :

• La lumière se propage en ligne droite dans un milieu homogène.
• La lumière se réfléchit et se réfracte selon les lois de Descartes.

Ce n'est qu'une première approximation. Dès que les dimensions des objets sont comparables à la longueur d'onde de la lumière, les phénomènes de diffraction modifient l'aspect des images.

Habituellement l'optique géométrique se limite à l'étude du domaine des vibrations lumineuses visibles. Selon les sources utilisées la lumière est monochromatique ou polychromatique.
Une lumière monochromatique produit sur l'œil une sensation de couleur fonction de sa période.
Les radiations visibles par l'œil humain ont des périodes comprises entre 1,3.10⁻¹⁵ s (violet) et 2,7.10⁻¹⁵ s (rouge).
Les fréquences (N = 1 / T) varient entre 3,7.10¹⁴ (rouge) et 7,7.10¹⁴ (violet).
Dans le vide, toutes les radiations se propagent à la vitesse c = 299 792 458 m/s.
La longueur d'onde λ = C.T (distance parcourue pendant une période) permet également de caractériser une lumière monochromatique. Elle varie entre 0,4 μ (violet) et 0,8 μ (rouge).

  Principe de la propagation rectiligne

L'examen des ombres ou d'un rayon laser montrent que dans un milieu homogène la lumière se propage en ligne droite.

Source ponctuelle :
C'est une source de lumière de très petites dimensions. Un petit trou percé dans un écran opaque, éclairé par une source intense ou le foyer d'un arc à Xénon sont des modèles de sources ponctuelles.
Rayon lumineux :
C'est une portion de droite suivie par la lumière. Une bonne approximation est donnée par un rayon laser.
Faisceau lumineux :
C'est un ensemble de rayons lumineux.
Faisceau parallèle :
Il est constitué de rayons parallèles. Une source situé à l'infini donne un faisceau parallèle.
Faisceau coniques :
Les rayons d'un faisceau conique passent par un même point.
Si la lumière part du sommet, le faisceau est divergent.
Si elle se dirige vers le sommet, le faisceau est convergent.
Dioptre :
Un dioptre est la surface de séparation entre deux milieux homogènes et isotropes.

  Lois de Descartes

 Indice absolu d'un milieu homogène

C'est le rapport entre la vitesse V de la lumière dans ce milieu et la vitesse de la lumière dans le vide N = c / V.
Dans les conditions normales (T = 0°C et p = 1013 mbar) l'indice absolu de l'air est N = 1,000292 pour λ = 0,587 µ.
La loi de Gladstone dit que le rapport (N − 1) / µ est constant. Donc pour un gaz (N − 1) est proportionnel à la pression et inversement proportionnel à la température absolue.
On fait en général l'approximation que l'indice de l'air est N = 1.

Valeurs des quelques indices

Eau 1,33 Cryolithe 1,33 Cornée 1,38 Verre ordinaire 1,50

Verres optiques 1.45 - 1,85 Oxyde de Titane 2,30 Sulfure de Zinc 2,35 Diamant 2,4

.
Lois de Descartes

On considère deux milieux homogènes et isotropes d'indices absolus N1 et N2 séparés par un dioptre. Un rayon AI monochromatique frappe le dioptre en I. Le rayon AI et la normale en ID au dioptre définissent un plan qui est le plan d'incidence. En général une partie du rayon est réfléchie et une partie est transmise. IB est le rayon réfléchi et IC est le rayon réfracté.

En même temps que Snell, Descartes qui pensait que la lumière était constitué par des grains matériels a établi de façon géométrique dans sa "Dioptrique" les lois suivantes :

Les rayons réfléchis et réfractés sont contenus dans le plan d'incidence.

Les angles d'incidence i et de réflexion j sont opposés : j = − i

Les angles d'incidence i et de réfraction r sont liés par la relation N1.sin i = N2.sin r

Ces lois sont symétriques et ne font pas intervenir le sens de propagation de la lumière.
Par conséquent on peut énoncer le principe du retour inverse de la lumière :

Le trajet suivi par la lumière est indépendant de son sens de propagation.

Forme vectorielle des lois de la réfraction

Soient N le vecteur normal unitaire à la surface, U le vecteur directeur unitaire incident et V le vecteur directeur unitaire réfracté.
Ces trois vecteurs sont coplanaires donc les produits vectoriels U ^ N et V ^ N sont colinéaires comme U et V sont reliés par la relation N1.sin i = N2.sin r, il est équivalent d'écrire : N1.U ^ N = N2.V ^ N.
Donc N1.U − N2.V = k.N et la multiplication scalaire de cette relation par N donne finalement :

N2.V = N1.U + (N2.cos i2 − N1.cos i1).N

Soient N le vecteur normal unitaire à la surface, U le vecteur directeur unitaire incident et V le vecteur directeur unitaire réfléchi.
Le vecteur U − V doit être colinaire avec N : (U − V) = k.N
La multiplication scalaire de cette relation par N donne (U − V).N = k.N.N = k = 2.cos i

U − V = 2.N.cos i

Si le choix des lois de Descartes est souvent fait pour la construction de l'optique géométrique, d'autres postulats permettent également cette construction.

  Principe d'Huygens

Une onde est une perturbation (scalaire ou vectorielle) qui se propage dans un milieu avec une vitesse v. Une surface d'onde est le lieu des points atteints par la vibration au même instant. On peut représenter une onde plane par des " plans d’onde " qui caractérisent une singularité de la perturbation : on peut repérer par exemple un ventre (ou un nœud) d’amplitude, de vitesse, de pression, de champ électrique… selon la nature de l’onde étudiée.

La propagation étant due à un mécanisme agissant de proche en proche, d'après le principe d'Huygens-Fresnel, chaque point de la surface d'onde se comporte comme une source secondaire qui émet une onde sphérique. La surface d'onde à l'instant t + dt est la superposition de toutes ces ondelettes de rayon v.dt. La surface d'onde à l'instant t + dt est la courbe enveloppe des ondes émises par les sources secondaires.
On montre à partir des équations de Maxwell que les rayons (trajectoires de l'énergie) sont normaux aux surfaces d'onde. La distance entre deux plans d’onde est la longueur d’onde λ (période spatiale). Elle est liée à la période T de la vibration (période temporelle) par la relation : λ = v.T

Réfraction des ondes

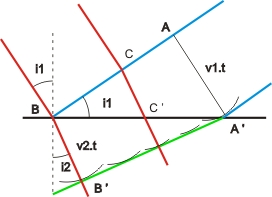On considère deux milieux, séparés par un dioptre plan, caractérisés par des vitesses de propagation v1 et v2. Dans le milieu supérieur, se propagent des ondes planes qui arrivent sur le dioptre avec l'incidence i1. La distance entre deux plans d'onde dans le milieu supérieur est v1.t. Dans le milieu inférieur, la surface d'onde peut être considérée comme l'enveloppe des sources secondaires émises par les points du dioptre compris entre A' et B. Le point C' est atteint au bout de τ = CC' / v1 = k.BC' / BA' = k.u L'ondelette émise dans le milieu inférieur a pour rayon r = v2(t − τ). r = v2.k(1 − u). Ce rayon est proportionnel à C'A'. Les ondelettes secondaires sont vues de A' sous l'angle i2 : L'onde réfractée est plane et sin(i2) = BB' / BA' = τ / BA' Comme sin(i1) = v1.t / BA', il vient : sin(i1).v2 = sin(i2).v1

Si l'on pose N = c / v, on retrouve la relation N1.sin(i1) = N2.sin (i2).

Illustration du principe d'Huygens

  Construction des rayons

A partir du principe d'Huygens et des lois de Descartes , on peut déduire deux méthodes graphiques de construction des rayons lumineux réfractés.

Construction d'Huygens :

Pour cette construction, on utilise la surface d'onde. C'est le lieu des points atteints par la lumière issue d'une source ponctuelle au bout du temps unité. Dans un milieu isotrope, la surface d'onde est une sphère dont le rayon est l'inverse de l'indice du milieu. Le plan d'onde, dans une direction donnée, est tangent à la surface d'onde et dans un milieu isotrope, les rayons lumineux sont normaux aux plans d'onde.
Pour construire le rayon réfracté lors de la traversée d'un dioptre, on considère une source secondaire d'Huygens, située sur le dioptre au point d'incidence.
De ce point, on trace la surface d'onde dans les deux milieux.
A partir du rayon incident, on déduit la position du plan d'onde incident MT et donc du plan d'onde émergent NT (Ils sont émis au même instant).
Enfin, on peut tracer le rayon émergent ON (normal au plan d'onde émergent).
Cette construction est équivalente à la relation : n₁.sin(i₁) = n₂.sin(i₂).
Dans le cas n₁ > n₂, la construction n'est possible que si le point T est situé à l'extérieur de la sphère de rayon n₂.
Cette condition définit l'angle "limite". Sinon, il y a réflexion totale sur le dioptre.

Construction de Descartes :

On utilise la surface des indices. C'est la surface engendrée par un rayon vecteur dont la longueur est celle de l'indice dans la direction étudiée. Dans un milieu isotrope, la surface des indices est une sphère de rayon égal à l'indice du milieu.
Du point d'incidence choisi comme centre, on trace les sphères de rayons n₁ et n₂. M est l'intersection du rayon incident avec la sphère de rayon n₁. De M on abaisse la perpendiculaire sur le dioptre. Cette droite MT traverse (sauf cas de réflexion totale) la sphère de rayon n₂ en N qui définit la direction du rayon émergent ON.
Cette construction simple permet de traduire géométriquement la loi de Descartes. Il est plus difficile que pour la construction d'Huygens de lui donner un sens physique.

  Principe de Fermat

Chemin optique :

Le temps mis par la lumière pour parcourir l'élément de longueur ds d'un rayon est dt = ds / v.
Le temps mis pour aller d'un point A à un point B est donc :

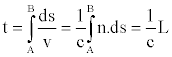
L'intégrale L de n.ds est le chemin optique (AB) entre les points A et B.

Principe de Fermat :

Entre deux points A et B, il existe une infinité de chemins possibles. Le principe de Fermat dit que :

Pour aller de A à B, la lumière emprunte un chemin tel que le chemin optique est extremum.
Fermat pensait que le chemin optique était toujours minimum. En fait il peut aussi être maximum.
On peut écrire ce principe sous les formes dL = 0 ou L.dL = 0.

Propagation rectiligne :
Considérons un milieu homogène.
L'indice étant constant, si D est la distance entre A et B, le chemin optique est n.D. Comme la droite AB correspond au minimum de D, dans un milieu homogène, la lumière se propage en ligne droite.

Lois de Descartes :
Un dioptre plan sépare deux milieux d'indices N1 et N2. Un rayon lumineux va de A₁ situé dans le milieu d'indice N1 et va en A₂ dans le milieu d'indice N2. On cherche la position du point J où le rayon traverse le dioptre.
Le chemin optique est L = N1.A₁J + N2.A₂J

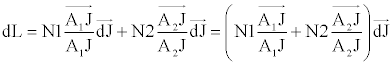
Pour que L.dL soit nul, il faut que :

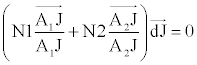
Le vecteur qui correspond au premier terme est donc orthogonal au dioptre : Le rayon appartient au plan passant par A₁ et A₂ et normal au dioptre : Les rayons incident et réfracté sont dans un même plan.

Si n est le vecteur normal au dioptre en J , on a aussi :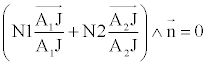

Si on pose I₁ angle entre JA₁ et n et I₂ angle entre JA₂ et n, on en déduit que N1.sin I₁ = N2 sin I₂

Cette démonstration, écrite sous sa forme vectorielle, est due à Maupertuis qui a généralisé le principe de Fermat en principe de moindre action.

Exemples d'applications du principe de Fermat :

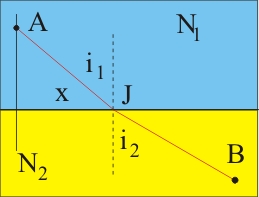On peut dans cet exemple retrouver simplement les lois de Descartes à partir du principe de Fermat. Le chemin optique est L = N1.AJ + N2.JB. L = N1.(X² + Ya²)½ + N2.((Xb − X)² + Yb²)½. L'extremum de L a lieu quand sa dérivée est nulle. dL = 0 = N1.X / (X² + Ya²)½ + N2(Xb − X) / ((Xb − X)² + Yb²)½. Or sin(i1) = X / AJ et sin(i2) = (Xb − X) / JB.   On en déduit que : N1.sin I1 = N2.sin I2

Le second exemple concerne les miroirs sphériques et le dioptre sphérique. Pour les miroirs concaves, le chemin optique est maximum alors que pour les miroirs convexes et pour le dioptre sphérique, il est minimum.
Vérifier que pour les miroirs, l'extremum de L correspond à l'égalité des angles d'incidence et de réflexion.
Vérifier que pour le dioptre sphérique, le minimum de L se produit quand la relation N₁.sin I₁ = N₂.sin I₂ est vérifiée et que pour N₁ = N₂ = 1, la lumière se propage en ligne droite..

Sur la figure, le trait vert est le rayon passant par le point d'incident. Les angles dessinés en vert et jaune sont donc les angles d'incidence et de réflexion.

  Approximation de Gauss

La relation de Descartes N1.sin(i) = N2.sin (r) n'est pas linéaire. Si les angles sont petits, il est possibles confondre les sinus et les angles. On obtient alors la relation de Kepler N1.i = N2.r
Pour un système centré, cette approximation est valide pour les rayons lumineux peu inclinés sur l'axe optique.
On dit alors qu'on se place dans le domaine paraxial ou dans l'approximation de Gauss.
Cette approximation simplifie considérablement l'étude des systèmes optiques qui deviennent linéaires.