On considère une poutre rectangulaire d'épaisseur e, de largeur l et de longueur L.
Soient S la section, µ la masse volumique, E le module d'Young et I = l.e3/12 l'inertie de la section droite de la poutre dans la direction de la largeur.
On démontre (voir par exemple : Vibrations des milieux continus Jean-Louis Guyader (Hermes)) que l'amplitude Y(x,t) du déplacement transversal d'une section droite de la poutre est donné, si on néglige l'amortissement par l'équation aux dérivées partielles
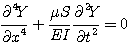 (1)
(1)
La solution de cette équation est fonction des conditions aux limites et des conditions initiales.
On se limite aux solutions de la forme Y(x,t) = y(x).cos(ω.t).
Conditions aux limites : Chaque extrémité peut être libre, appuyée, guidée ou encastrée.
On se limite ici à la détermination des modes propres pour les cas encastrée-libre et encastré-encastré.
Conditions initiales : La solution est une combinaison linéaire de tous les modes propres, l'amplitude de chaque mode propre étant fonction des conditions initiales.
Utilisation :
Les courbes représentent l'évolution de la forme de la poutre pour le mode d'indice n en fonction du temps. A cause de la grande plage de variation pour la fréquence, j'ai conservé dans la simulation une valeur de ω constante dans le terme cos(ω.t)
Les valeurs R(n) affichées sont les solutions de l'équation transcendante qui intervient dans la résolution du problème.
Les valeurs f(n) sont les valeurs des fréquences propres qui correspondent aux valeurs numériques utilisées.
Les boutons radio permettent la sélection des deux cas étudié.
Les boutons [+] et [−] permettent de modifier l'indice du mode propre qui est visualisé.
Pour permettre une meilleure visualisation, l'échelle verticale est fortement dilatée.
Valeurs numériques utilisées : l = 2 cm; e = 0,5 mm; L = 25 cm; µ = 7,8 g/cm3; E = 21 1010 N/m2.
Cliquer dans le cadre de l'applet pour geler l'animation.
