La liaison chimique

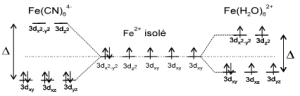
L'ion Ti (+III) solvaté

On prend comme exemple simple le processus de solvatation dans l'eau de l'ion $\text{T}{{\text{i}}^{\text{3+}}}\text{ }\!\!~\!\!\text{ (ion 3}{{\text{d}}^{\text{1}}}\text{)}$ .

Les DNL des molécules d'eau sont attirés par la charge positive du cation et le complexe octaédrique $\text{Ti(}{{\text{H}}_{\text{2}}}\text{O)}_{\text{6}}^{\text{3+}}$ se forme.

Sous l'action du champ électrique des ligands (champ cristallin), les niveaux d'énergie de l'ion central se trouvent modifiés.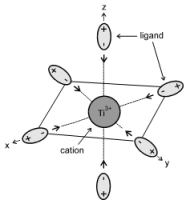

La forme et la symétrie du complexe décident des orbitales atomiques de l'ion qui sont concernées

(la somme des énergies des niveaux disponibles restant constante) :

  • les orbitales atomiques axiales $\text{3}{{\text{d}}_{{{\text{x}}^{\text{2}}}\text{-}{{\text{y}}^{\text{2}}}}}\text{et}\text{ 3}{{\text{d}}_{{{\text{z}}^{\text{2}}}}}$ vont se trouver les plus perturbées (leur énergie augmente)

  • les 3 autres orbitales atomiques $\text{3}{{\text{d}}_{\text{xy}}}\text{,}\text{3}{{\text{d}}_{\text{xz}}}\text{,}\text{3}{{\text{d}}_{\text{yz}}}$ voient leur énergie diminuer.

  • La valeur de l'énergie $\Delta $ qui mesure l'éclatement des niveaux dépend directement du champ des ligands et donc de la nature du ligand :

    • ligands à champ fort : $\text{C}{{\text{N}}^{\text{-}}}\text{, N}{{\text{O}}^{\text{2-}}}$

    • ligands à champ faible : ${{\text{H}}_{\text{2}}}\text{O, N}{{\text{H}}_{\text{3}}}\text{, C}{{\text{l}}^{\text{-}}}$

Les électrons périphériques de l'ion central (ici 1 e-) vont se répartir dans le nouveau schéma.

On constate un gain de stabilité (énergie plus basse de l'électron).

La couleur et le magnétisme des éléments de transition s'interprète bien dans le cadre du champ cristallin :

  • L'absorption par l'électron d'une énergie $\text{E=h }\!\!\upsilon\!\!\text{ }$ dans le spectre visible excite l'électron sur un des niveaux supérieurs disponibles (il se désexcite rapidement de manière non radiative).

  • La disparition, de la lumière visible, par absorption de la longueur d'onde verte

    $$\text{ }\!\!\lambda\!\!\text{ =0}\text{.51 }\!\!\mu\!\!\text{ m,      }\!\!\Delta\!\!\text{ }\approx \text{234 kJ}\text{.mol}{{\text{e}}^{\text{-1}}}\text{, 1 kJ}\text{.mol}{{\text{e}}^{\text{-1}}}\text{=83}\text{.6 c}{{\text{m}}^{\text{-1}}}$$

    explique la couleur pourpre de cette solution (couleur complémentaire de la couleur absorbée), la largeur de la raie d'absorption est due aux vibrations d'origine thermique dans le liquide .

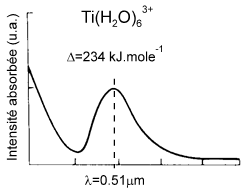Les valeurs relatives de $\Delta $ et de l'énergie d'appariement (énergie nécessaire pour maintenir 2 électrons associés en doublet : $\text{229 }\!\!~\!\!\text{ kJ}\text{.mol}{{\text{e}}^{\text{-1}}}$ pour $\text{F}{{\text{e}}^{\text{2+}}}\text{, ion 3}{{\text{d}}^{\text{6}}}$ ) vont décider si le complexe est à :

  • “ haut spin ” comme $\text{Fe(}{{\text{H}}_{\text{2}}}\text{O)}_{\text{6}}^{\text{3+}}$

    (4 électrons célibataires,   paramagnétique)

    $\text{ }\!\!\Delta\!\!\text{ }\approx \text{120 kJ}\text{. mol}{{\text{e}}^{\text{-1}}}$

  • “ bas spin ” comme $\text{Fe(CN)}_{\text{6}}^{\text{3+}}$

    (0 électron célibataire,    diamagnétique)

    $\text{ }\!\!\Delta\!\!\text{ }\approx \text{395 kJ}\text{. mol}{{\text{e}}^{\text{-1}}}$

PrécédentPrécédentFin
AccueilAccueilRéalisé avec Scenari (nouvelle fenêtre)