La réaction chimique, thermodynamique chimique, cinétique chimique

Notée ${{\text{ }\!\!\Delta\!\!\text{ }}_{\text{f}}}{{\text{H}}^{\text{o}}}$; elle correspond à l'enthalpie standard de formation d'un corps composé par la réaction de formation de ce corps à partir des éléments pris dans leur état standard.

Par convention, ${{\text{ }\!\!\Delta\!\!\text{ }}_{\text{f}}}{{\text{H}}^{\text{o}}}$ corps pur simple dans l'état standard $=\text{ }0\text{ }J.mo{{l}^{-1}}$ quel que soit T.

Choix du corps pur simple

Exemple : pour l'élément oxygène, on prend ${{\text{O}}_{\text{2}}}$ . Pour le fer, il existe deux variétés cristallines. A l'état standard, l'élément fer est constitué par le fer $\alpha $.

Remarque : à chaque fois dans les tables que ${{\text{ }\!\!\Delta\!\!\text{ }}_{\text{f}}}{{\text{H}}^{\text{o }\!\!~\!\!\text{ }}}\text{= 0}$ c'est un corps de référence.

Exemples d'équations bilans et d'enthalpies de formation

• ${{\text{O}}_{\text{2}}}$ pour toute température, ${{\text{O}}_{\text{2}}}$ gaz = référence cependant si on veut calculer ${{\text{ }\!\!\Delta\!\!\text{ }}_{\text{f}}}{{\text{H}}^{\text{o}}}$ (${{\text{O}}_{\text{2}}}$ liquide)

• ${{\text{O}}_{\text{2}}}\left( \text{g} \right)\text{ = }{{\text{O}}_{\text{2}}}\left( \text{liq} \right)\ \ \ \ \ \ \ {{\text{ }\!\!\Delta\!\!\text{ }}_{\text{f}}}{{\text{H}}^{\text{o }\!\!~\!\!\text{ }}}\left( {{\text{O}}_{\text{2liq}}} \right)\text{ = }{{\text{H}}^{\text{ }\!\!{}^\circ\!\!\text{ }}}\left( {{\text{O}}_{\text{2}}}\ell \right)\text{ - }{{\text{H}}^{\text{ }\!\!{}^\circ\!\!\text{ }}}\left( {{\text{O}}_{\text{2}}}\text{g} \right)$ mais ${{\text{H}}^{\text{ }\!\!{}^\circ\!\!\text{ }}}\left( {{\text{O}}_{\text{2}}}\text{g} \right)\text{ = 0}$ donc ${{\Delta }_{f}}{{H}^{o~}}\left( {{O}_{2liq}} \right)\ne 0$

  Il faut donc faire attention à l'état physique !!!

• Formation de l'éthanol : $2{{C}_{graphite(s)}}+3{{H}_{2(g)}}+{\scriptstyle{}^{1}/{}_{2}}{{O}_{2(g)}}\to C{{H}_{3}}C{{H}_{2}}O{{H}_{(l)}}$ ${{\Delta }_{f}}{{H}^{o}}=-277\text{ }kJ/mol$

• Formation de l'oxyde de fer III : $2Fe{{S}_{(s)}}+{3}/{2}\;{{O}_{2(g)}}\to F{{e}_{2}}{{O}_{3}}_{(s)}$ et ${{\Delta }_{f}}{{H}^{o}}=-\text{ }823.5\text{ }kJ/mol$

Notée ${{\text{ }\!\!\Delta\!\!\text{ }}_{\text{r}}}{{\text{H}}^{\text{o}}}$

Pour une réaction quelconque symbolisée par: $\sum\limits_{i}{{{\nu }_{i}}}{{A}_{i}}\to \sum\limits_{k}{{{\nu }_{k}}}{{A}_{k}}$

$${{\Delta }_{r}}{{H}^{0}}=\sum\limits_{k}{{{\nu }_{k}}{{\Delta }_{f}}H_{T}^{0}({{A}_{k}})-\sum\limits_{i}{{{\nu }_{i}}{{\Delta }_{f}}H_{T}^{0}({{A}_{i}})}}$$

Cette relation est vraie quelle que soit T.

On peut calculer une grandeur standard de réaction en connaissant les grandeurs standard de formations des produits et des réactifs.

Exemple : écrire la réaction de combustion de l'acide éthanoïque et calculer la variation d'enthalpie de la réaction :

$\begin{align}& C{{H}_{3}}COO{{H}_{(l)}}+2{{O}_{2(g)}}\to 2C{{O}_{2(g)}}+2{{H}_{2}}{{O}_{(l)}} \\& {{\Delta }_{r}}{{H}^{o}}=\text{ }2{{\Delta }_{f}}{{H}^{o}}_{(CO2(g))}+\text{ }2{{\Delta }_{f}}{{H}^{o}}_{(H2O(l))}-{{\Delta }_{f}}{{H}^{o}}_{(CH3COOH(l))}-\text{ }2{{\Delta }_{f}}{{H}^{o}}_{(O2(g))} \\& {{\Delta }_{r}}{{H}^{o}}_{(298K)}=\text{ }-871.6\text{ }kJ/mol \\\end{align}$

Changement d'état

Il s'agit d'une transformation physique.

• Fusion : passage de l'état solide à l'état liquide ; Ex : ${{H}_{2}}O\left( s \right)\to {{H}_{2}}O\left( l \right)$

  L'inverse de cette transformation étant la solidification.

• Vaporisation : passage de l'état liquide à l'état gazeux ; Ex : ${{H}_{2}}O\left( l \right)\to {{H}_{2}}O\left( g \right)$

  L'inverse de cette transformation étant la liquéfaction.

• Sublimation : passage de l'état solide à l'état gazeux ; Ex : ${{I}_{2}}\left( s \right)\to {{I}_{2}}\left( g \right)$

  L'inverse de cette transformation étant la condensation.

Il peut s'agir aussi d'un changement de structure cristalline ; Ex : $C\left( g \right)\to C\left( d \right)$

On dit que ce sont des variétés allotropiques.

Notation de enthalpies de changement d'état

Elles sont notées $\text{ }\text{ }\!\!\Delta\!\!\text{ }{{\text{ }}_{\text{fus}}}\text{H ou}\text{ }{{\text{L}}_{\text{f}}}\text{ }\text{, }\text{ }\!\!\Delta\!\!\text{ }{{\text{ }}_{\text{vap}}}\text{H ou}\text{ }{{\text{L}}_{\text{vap}}}$ .encore appelées chaleurs latentes de changement d'état.

Si la $\text{ }\text{ }\!\!\Delta\!\!\text{ }{{\text{ }}_{\text{fus}}}\text{H ou }{{\text{L}}_{\text{f}}}\text{ vaut -248 kJ/mol}$ par exemple, l'enthalpie de la transformation inverse vaut +248kJ/mol.

Il s'agit de l'enthalpie standard de la réaction associée à l'ionisation d'un atome gazeux en ion positif (gazeux) :

$$X\left( g \right)\to {{X}^{+}}\left( g \right)\text{ }+\text{ }{{e}^{-}}\text{ ; }\Delta H_{ion}^{0}>0$$

(il faut fournir de l'énergie pour arracher un électron).

Il s'agit en toute rigueur de l'énergie interne à 0K de cette réaction.

Il s'agit de l'enthalpie standard de la réaction associée à l'addition d ‘un électron à l'atome gazeux pour former un ion négatif gazeux : $X\text{ }\left( g \right)\text{ }+\text{ }{{e}^{-}}\to {{X}^{-}}\left( g \right)$ , c'est en fait l'opposé de l'énergie interne à 0K.

${{\text{E}}_{\text{att}}}\text{= E}_{\text{x}}^{\text{-}}\text{- }{{\text{E}}_{\text{X}}}$ si $~{{\text{E}}_{\text{att}}}\text{0}$ alors $~\text{E}_{\text{x}}^{\text{-}}\text{}{{\text{E}}_{\text{X}}}$ donc ${{X}^{-}}$ est moins stable que ${{\text{X}}^{\text{-}}}$ et inversement si ${{E}_{att}}>0\text{ }~\text{ ; }E_{x}^{0}>{{E}_{X}}$ alors ${{X}^{-}}$ est plus stable que $\text{X}$.

On définit l'affinité électronique AE comme l'opposé de l'enthalpie d'attachement électronique.

• AE est d'autant plus grande que l'anion ${{X}^{-}}$ est stable.

• Valeur élevée pour les halogènes (ion halogénure ${{X}^{-}}\left( g \right)\text{ }n{{s}^{2}}n{{p}^{6}}~~~~\left[ Gaz\text{ }rare \right]$).

Définition

L'énergie de liaison de la liaison A-B est l'énergie interne à 0K de la réaction :

$$AB\left( g \right)\to {{A}^{.}}\left( g \right)\text{ }+\text{ }{{B}^{.}}\left( g \right)$$

• On l'assimile à l'enthalpie de réaction.

• Elle est caractéristique d'une liaison chimique .

• Elle est positive car il faut fournir de l'énergie pour rompre une liaison.

  On la note ${{\text{E}}_{\text{l}}}$.

En pratique, il n'est pas possible d'isoler les atomes et une telle réaction est purement hypothétique. La réaction inverse est la réaction de dissociation.

Distinction liaison faible/liaison forte

Calcul d'une enthalpie de réaction à partir des énergies de liaison

Exemple : $2{{H}_{2}}\left( g \right)\text{ }+\text{ }{{O}_{2}}\left( g \right)\to 2{{H}_{2}}O(g)$

Il y a rupture de deux liaisons H-H et O=O pour donner des atomes isolés 4H et 2O puis formation de 4 nouvelles liaisons $\text{H-O }\left( \text{2 }{{\text{H}}_{\text{2}}}\text{O} \right)$

Données : ${{\text{ }\!\!\Delta\!\!\text{ }}_{\text{diss}}}{{\text{H}}^{\text{ }\!\!{}^\circ\!\!\text{ }}}\left( \text{OH} \right)\text{ = 428 kJ/mol }\!\!~\!\!\text{ ; }{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{diss}}}{{\text{H}}^{\text{ }\!\!{}^\circ\!\!\text{ }}}\left( {{\text{H}}_{\text{2}}} \right)\text{ = 436 kJ/mol }\!\!~\!\!\text{ ; }{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{diss}}}{{\text{H}}^{\text{ }\!\!{}^\circ\!\!\text{ }}}\left( {{\text{O}}_{\text{2}}} \right)\text{ = 495 kJ/mol}$

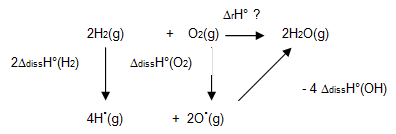
$${{\Delta }_{r}}{{H}^{o}}_{{}}=\text{ }-\text{ }4{{\Delta }_{diss}}H{}^\circ \left( OH \right)\text{ }+2{{\Delta }_{diss}}H{}^\circ \left( {{H}_{2}} \right)\text{ }+{{\Delta }_{diss}}H{}^\circ \left( {{O}_{2}} \right)\text{ }=\text{ }-\text{ }345\text{ }kJ/mol$$

Définition

L'énergie réticulaire est l'énergie interne à 0K de la réaction de dissociation d'une mole de cristal en ses ions constitutifs à l'état gazeux supposés immobiles et séparés.

${{C}_{x}}{{A}_{y}}\left( s \right)\to x{{C}^{p+}}\left( g \right)\text{ }+\text{ }y{{A}^{q-}}\left( g \right)$ , elle est positive.

Exemple : $NaCl\left( s \right)\to N{{a}^{+}}\left( g \right)\text{ }+\text{ }C{{l}^{-}}\left( g \right)$

Détermination expérimentale: cycle de Born Haber Sur l'exemple de KCl :

On construit deux chemins différents menant du même état initial $K\left( s \right)\text{ }+\text{ }{\scriptstyle{}^{1}/{}_{2}}C{{l}_{2}}\left( g \right)$ au même état final $\text{KCl}\left( \text{s} \right)$.

• Le premier direct correspond à l'enthalpie de formation ;

• le deuxième indirect correspond à différentes enthalpies mesurables.

Données :

• ${{\text{ }\!\!\Delta\!\!\text{ }}_{\text{f}}}\text{H}_{\text{KCl(s)}}^{\text{0}}\text{=-453kJ/mol ; }{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{sub}}}\text{H}_{\text{K}}^{\text{0}}\text{=89kJ/mol ; }{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{ion}}}\text{H}_{\text{K}}^{\text{0}}\text{=418kJ/mol}$

• ${{\text{ }\!\!\Delta\!\!\text{ }}_{\text{diss}}}\text{H}_{\text{C}{{\text{l}}_{\text{2}}}}^{\text{0}}\text{=244kJ/mol ; Ae= 349 kJ/mol}$

${{\text{E}}_{\text{r }\!\!\acute{\mathrm{e}}\!\!\text{ t}}}\text{=}{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{f}}}\text{H}_{\text{KCl(s)}}^{\text{0}}\text{+}{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{sub}}}\text{H}_{\text{K}}^{\text{0}}\text{+}{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{ion}}}\text{H}_{\text{K}}^{\text{0}}\text{+1/2}{{\text{ }\!\!\Delta\!\!\text{ }}_{\text{diss}}}\text{H}_{\text{C}{{\text{l}}_{\text{2}}}}^{\text{0}}\text{-Ae=715kJ/mol}$