Retour| Retour |
Dosage potentiométrique du fer II par le permanganate de potassium |
On décrit ici la méthode de dosage potentiométrique du Fer +II (dont on cherche le titre) par une solution de permanganate de potassium ainsi que le calcul de de la concentration recherchée.
Les séquences vidéos sont annoncées par
à l'endroit où elles complètent le texte et les images
explicatifs.
Au premier appel de vidéo, laissez au lecteur vidéo le temps de
se charger (quelques secondes), N'oubliez pas de refermer la fenêtre vidéo.
| I. Principe du dosage | |||
| Tout d'abord, il faut identifier les réactants : quel est l'oxydant ? Quel est le réducteur ? Pour cela, on trace l'échelle des potentiels standards. | |||
 |
Les conditions expérimentales
|
||
| II. Le dosage | |||
On utilise un montage comportant :
Dans un premier temps, on verse le permanganate par ajoût de 0,5 mL et on observe la formation de la coloration violette (et sa disparition) au sein du bécher. On note pour chaque valeur du volume versé la valeur du potentiel après équilibre (celui-ci peut être long à atteindre lorsqu'on s'approche de l'équivalence), de manière à pouvoir tracer la courbe E = f(Volumeversé). On peut évidemment tracer cette courbe point par point au fur et à mesure des ajoûts (pendant le temps de mise en équilibre). |
|||
| Au voisinage du point d'équivalence, la couleur violette à tendance à persister, en même temps, les variations du potentiel deviennent plus importantes (et le temps de mise en équilibre du potentiel est plus long). |
On s'approche de l'équivalence |
||
| L'ajoût est ramené
à 0,1mL puis on finit à la goutte. L'équivalence est marquée par une couleur rose persistante (violet très dilué) et par un saut de potentiel. On note la valeur du volume de permanganate versé. |
A l'équivalence |
||
| On continue à faire des ajoûts
de 0,1mL tant qu'on reste dans le saut de potentiel. La couleur violette
du permanganate se renforce car il n'y a plus de Fer II pour le réduire, |
Après l'équivalence |
||
| On réaugmente l'ajoût à 0,5mL. On remarque que le potentiel ne varie plus de façon notable (la variation corespond à l'augmentation de la concentration en permanganate de potassium). Il faut cependant poursuivre les ajoûts suffisamment pour disposer d'un palier de potentiel nécessaire à l'exploitation de la courbe E = f(Volumeversé) . |
Fin du dosage |
||
|
Si vous souhaitez revoir l'intégralité
du dosage - Attention :
4mn45s - 10 Mo |
|||
| III. Interprétation des résultats | |||
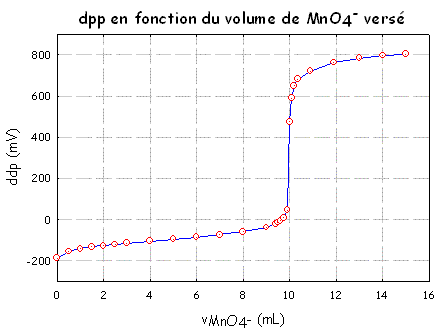
On ne peut mesurer que la différence de potentiel (ddp) entre 2 électrodes; l'électrode de référence au mercure I ayant un potentiel défini (0,648 V dans les conditions du dosage), toute variation du potentiel de la solution se traduit par une variation identique de la ddp de la solution. La solution de départ contenait la forme réduite du couple Fe3+/Fe2+ (E0 = 0,77 V). Le potentiel de cette solution est donc proche de E0. Quand on ajoute, le permanganate de potassium (forme oxydée du couple MnO4-/Mn2+ , E0 = 1,51 V) le potentiel de la solution augmente quand la quantité d'ions Fe2+ diminue. A l'équivalence, le potentiel varie brusquement car la différence des potentiels standards est grande et il n'y a plus d'ions Fe2+ pour réduire les ions MnO4- que l'on continue à ajouter (ce qui augmente le potentiel de manière continue). Si on porte en ordonnée la variation de la différence
de potentiel observée pendant le dosage, en fonction du volume
de permanganate versé, on obtient la courbe potentiométrique
du dosage de Fe2+ par MnO4- visible à
droite. |
 |
||
 |
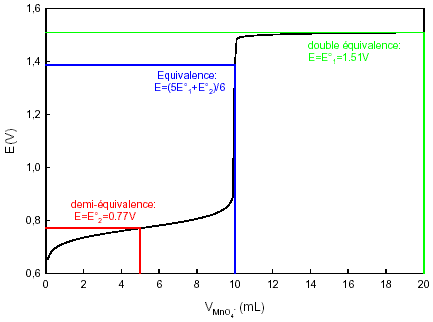Il faut donc déterminer le volume précis du point d'équivalence. Vous pourrez consulter le
document qui vous explique pourquoi dans ce dosage le point
d'équivalence est obtenu avec la relation : Il reste alors à déterminer le point de la courbe situé à la valeur EEq et à abaisser la verticale pour trouver le volume réellement versé à l'équivalence. On trouve vEq = 10,0 mL On applique la relation avec les valeurs correspondantes
pour déterminer la concentration c2 de la solution de
fer II Si on applique la relation de concentration  ,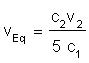
on va trouver c2= 0,10 mol/L |
||
| La concentration de départ de la solution de fer II était de 0,10 mol/L | |||
Retour
et
donne la relation de concentration.