Une orbite de Hohmann est une trajectoire qui permet de passer d'une orbite circulaire de rayon R₁ à une autre orbite circulaire coplanaire de rayon R₂ en utilisant seulement deux impulsions motrices.
L'orbite est une ellipse de périgée R₁ et d'apogée R₂.
Le grand axe de l'ellipse est a = ½.(R₁+ R₂) et son excentricité e = (R₁− R₂) / (R₁+ R₂) .

On examine le cas de l'orbite de transfert d'une sonde entre une orbite basse de la Terre et une orbite basse de Mars.
On fait les hypothèses suivantes : Les trajectoires de la Terre et de Mars sont des cercles coplanaires.
Le rayon de l'orbite terrestre vaut R_T = 150.10⁶ km et celui de l'orbite de Mars est R_M = 228.10⁶ km.
La période P_T de la Terre est de 365 jours et celle de Mars est P_M = 686 jours.
D'après la troisième loi de Kepler le rapport du carré de la période par le cube du demi-grand axe est constant :
T² / a³ = 4.π² / G.M (G = 6,67428.10⁻¹¹ constante de gravitation et M valeur de la masse centrale).
On en déduit la période de la sonde sur son orbite de transfert P_S = 510 jours.

Paramètres de l'orbite de Hohmann :
Demi-grand axe a = 189.10⁶ km.     Excentricité e = 0,2063     
Dans le repère défini par l'axe focal et le foyer (le Soleil), l'équation polaire de l'ellipse est ρ = P / (1 + e.cos(φ))
P est la paramètre de l'ellipse (P = a.(1 − e²)). φ est l'angle entre l'axe focal et le rayon vecteur.

On utilise l'équation du temps de Kepler : t = T.(ψ − e.sin(ψ)) / 2.π pour déterminer le mouvement de la sonde en fonction du temps.

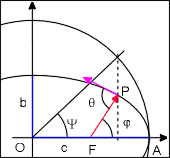
O est le centre de l'ellipse.
A est le périapse*. OA = a.
F est le foyer de l'ellipse
OF = c = a.e = (a² − b²)^½
FP = ρ est le rayon vecteur.
φ (angle AFP) est l'anomalie vraie.
ψ est l'anomalie excentrique.

La résolution par une méthode numérique de l'équation du temps donne ψ.
Les anomalies vraie et excentrique sont reliées par la relation :
Il est alors possible de déterminer la position P de la sonde sur son orbite au temps t.

Mouvements de la sonde :
La sonde placée en orbite basse de la Terre reçoit à l'instant t = 0 une impulsion qui augmente sa vitesse et son moment cinétique et lui permet de passer sur l'orbite de Hohmann. La sonde est a cet instant à son périgée. Elle met un temps T_S / 2 = 255 jours pour atteindre son apogée. Il faut que Mars soit à cet endroit à cet instant. On applique à nouveau une impulsion pour augmenter la vitesse et faire passer la sonde en orbite basse martienne.

Les présences simultanées de la sonde et de Mars à l'apogée de l'orbite de Hohmann impose que la planète Mars décrive un angle α = 134 ° = (½.P_S / P_M).360 depuis l'instant du passage de la sonde sur son orbite elliptique.
Les positions relatives de la Terre et de Mars qui correspondent à cette situation ne sont pas très fréquentes.
La pulsation de la Terre est ω_T = 6,2831 Rd / an. Celle de Mars est ω_M = 3,340 Rd / an.
Entre deux oppositions (ou entre deux situations favorables au lancement) , la Terre décrit un tour de plus que Mars. On a donc t. ω_T = t. ω_M + 2π.
La durée entre deux oppositions est donc t = 2π / ( ω_T − ω_M) soit environ 2 années et 49 jours (779 jours).