L'onde associée à une particule est l'onde stationnaire :
ψ = ψ0(x)sin(ωt)
dont la pulsation est liée à l'énergie par la relation :
E = ħ.ω
et dont le carré de l'amplitude représente la probabilité de présence
dP = ψ2(x).dx
Un oscillateur harmonique à une dimension correspond au potentiel
V = ½.k.x2 (en effet F = −k.x).
La fonction d'onde ψ(x) est solution de :
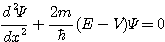
On montre que Ψ(x) = y(x)e−ax² et que pour obtenir une solution convergente , y doit être un polynôme de degré N.
En utilisant la coordonnée réduite
X = x.(mk)½ / ħ
y(x) doit être la solution de :
y'' − 2.X.y' + 2.N.y = 0.
Les polynômes y(x) sont les polynômes d'Hermite.
Le fait que y(x) soit un polynôme impose que les valeurs possibles pour l'énergie sont données par :
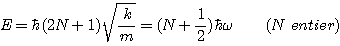
La particule ne peut être au repos : son énergie minimale est E = ½ ħ.ω
Pour un oscillateur harmonique classique, la probabilité de présence est maximale pour les valeurs extrêmes de l'amplitude (vitesse nulle) et elle est minimale pour une élongation nulle (vitesse maximale).
Pour un oscillateur quantique, les phénomènes sont très différents surtout pour les faibles valeurs de N. Quand N augmente, on retrouve le fait que la probabilité de présence est maximale au voisinage de X0 = ±(2N + 1)½ .
Utilisation :
Les sliders permettent de modifier les valeurs de la constante de rappel K et de la masse M (les unités sont arbitraires).
Les traits bleus correspondent aux niveaux d'énergie autorisés.
Les courbes en rouge représentent la probabilité de présence de la particule qui est le carré de la fonction d'onde.
L'axe des abscisses est gradué en coordonnées réduites X.
La parabole dessinée en noir correspond aux valeurs de X0 = (2N + 1)½.
