Ce programme permet de visualiser les opérations élémentaires du calcul vectoriel dans un repère triorthonormé Oxyz.
Dans ce texte, les vecteurs sont représentés en gras.
Les vecteurs ont tous comme origine le point O. Les coordonnées de l'extrémité du vecteur V_i sont x_i, y_i et z_i.

Produit scalaire :
C'est le nombre scalaire défini par :

V₁.V₂ = V₁.V₂.cos(V₁,V₂)

Il est nul si les vecteurs sont orthogonaux.
La norme N d'un vecteur est la racine carrée du produit scalaire du vecteur par lui-même.

| V₁ |² = x₁.x₁ + y₁.y₁ + z₁.z₁

Produit vectoriel :
C'est le vecteur :
V₃ = (V₁∧V₂) normal au plan des deux vecteurs V₁ et V₂ tel que le trièdre V₁, V₂ et V₃ est direct.
La norme de V₃ est || V₃ || = || V₁ || . || V₂ || . sin(V₁, V₂)

Les composantes de V₃ sont :
(y₁.z₂ − y₂.z₁)
(z₁.x₂ − x₁.z₂)
(x₁.y₂ − x₂.y₁).

La norme de V₃ est l'aire du parallélogramme construit avec les vecteurs V₁ et V₂.
V₃ est nul si les vecteurs sont colinéaires.

Produit mixte :
C'est le nombre scalaire défini par :      pm = (V₁,V₂,V₃) = (V₁.(V₂ ∧ V₃))
C'est le volume du parallélépipède construit sur les trois vecteurs.
C'est aussi la valeur du déterminant :

| V₁x   V₂x    V₃x |
| V₁y   V₂y    V₃y | = Δ
| V₁z   V₂z    V₃z |

Le produit mixte est nul si deux vecteurs sont colinéaires.

Double produit vectoriel :
C'est le vecteur :
D = V₁ ∧ (V₂ ∧ V₃) = (V₁ . V₃) V₂ − (V₁ . V₂) V₃.
Le vecteur P = V₂ ∧ V₃ est normal au plan Π contenant les vecteurs V₂ et V₃. Donc le vecteur D est contenu dans le plan Π.
D est donc de la forme D = α.V₂ + β.V₃
Le calcul des coefficients α et β plutôt pénible est ici seulement esquissé.

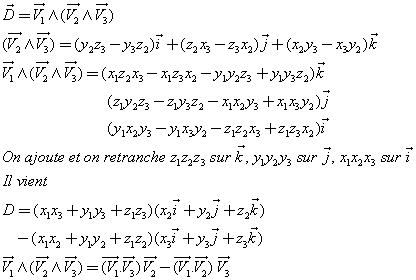
On montre de même que :
D' = (V₁ ∧ V₂) ∧ V₃ = (V₁ . V₃) V₂ − (V₂ . V₃) V₁.
En général D et D' sont différents.

Un exemple classique d'utilisation du double produit vectoriel est le calcul du moment d'une force qui résulte d'un produit vectoriel (force de Laplace ...)

On utilise aussi les produits de 4 vecteurs : (u∧v).( w∧x) = (u.w)(v.x) − (u.x)(v.w) (scalaire) et:
(u∧v) ∧ ( w∧x) = (u, v, x)w − (u, v, w)x qui est un vecteur.

Utilisation :

Glisser la souris dans le cadre pour modifier l'angle de vision.
Modifier les composantes des vecteurs avec les zones de texte.
Pour le produit vectoriel, un vecteur égal au tiers du vecteur produit V₃ est affiché en vert ainsi que le losange construit sur les deux vecteurs dont on fait le produit.
Pour le double produit vectoriel, un vecteur égal au tiers du vecteur P = V₂ ∧ V₃ est affiché en indigo ainsi qu'un vecteur égal au neuvième de D est affiché en bleu pale. Vérifier en orientant la figure que D, V₂ et V₃ sont coplanaires.