Un pont de Wheatstone est constitué de quatre résistances, d'un générateur de fem E et d'un détecteur (ici un voltmètre ayant une très grande impédance d'entrée).

R₁ et R₂ d'une part et R₃ et R₄ d'autre part constituent des diviseurs de la tension E d'alimentation du pont. On en déduit que :

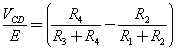
A l'équilibre (V_CD = 0), on a : R₁R₄ = R₂R₃

Les produits en croix des résistances sont égaux à l'équilibre du pont.

Dans le pont étudié ici, Ra et Rb sont des résistance fixes connues, R est une résistance variable de valeur connue et Rx est résistance de valeur inconnue.
Le voltmètre mesure la différence de potentiel de la diagonale du pont. Comme le courant dérivé dans cette branche est nul, il vient : U = E.(R / (Rb + R) − Rx / (Ra + Rx))
Si cette différence de potentiel est nulle, alors : Rx = R.Ra / Rb = K.R

Utilisation :
Le programme simule un tel pont.
Un click sur le bouton [Nouvelle Rx] provoque le calcul d'une valeur aléatoire de Rx.
Avec le slider de commande de R et en choisissant la valeur convenable du rapport K = Ra / Rb, recherchez l'équilibre du pont.
Un click sur le bouton [Réponse] affiche la valeur de Rx.
La résolution de R est égale à 5 Ω. Les résistances Ra et Rb sont des résistances à 0,5 %. Déterminez l'incertitude sur la valeur de Rx. Pour quelles conditions la sensibilité de pont est-elle la meilleure ?
Pour réaliser ce pont, il faut deux résistances fixes de précision et une résistance variable de précision.

Pont hors de l'équilibre :
On peut remplacer le pont par un générateur de Thévenin équivalent de Fem V_CD et de résistance interne R_T avec :
R_T = R₁R₂ / (R₁ + R₂) + R₃R₄ / (R₃ + R₄)
Si au voisinage de l'équilibre on fait varier légèrement les résistances on peut montrer que la tension V_CD est donnée par la relation

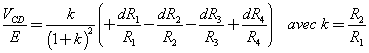
Cette relation est utilisée quand on emploie un pont de Wheatstone pour étudier la variation de résistance d'un capteur (sondes de température, jauges de déformation ...)