Dans ce multivibrateur deux transistors sont couplés par des liaisons capacitives reliant le collecteur de l'un à la base de l'autre. Les diodes LED sont facultatives. Les valeurs des résistances sont choisies pour permettre une saturation franche des transistors.
Si on examine le schéma du circuit on constate une forte ressemblance avec le schéma de la bascule Ecless-Jordan. Ce sont deux circuits comportant deux parties identiques avec une réaction positive. Pour la bascule le couplage est réalisé avec des résistances alors que pour l'astable il est réalisé avec des condensateurs.
Fonctionnement
A l'instant initial t, on suppose que T1 est bloqué et T2 saturé.
En t + ε on suppose que la base de T1 devient légèrement positive. T1 se sature et le potentiel de son collecteur passe brutalement de U à pratiquement 0 car la tension VCE d'un transistor saturé est de l'ordre de 0,1 V.
Le potentiel
de la base de T2 passe de VBE ≈ 0,65 V à VBE ≈ − U + 0,65 V car la charge du condensateur Q = C1.U du condensateur C1 n'a pas le temps de varier pendant la transition.
Le potentiel de la base de T2 devenant très négatif T2 se bloque. Le potentiel de son collecteur croît vers U. Le condensateur C2 se charge à travers Rc2 et l'espace émetteur-collecteur de T1 avec un constante de temps τ2 = Rc2.C2.
Le potentiel de la base de T1 reste légèrement positif se qui assure sa saturation.
Le condensateur C1 se charge à travers Rb2 et l'espace émetteur-collecteur de T1. Le potentiel de la base de T2 va croître avec un constante de temps τ1 = Rb2.C1. Quand Vb2 dépasse le tension VBE le système bascule vers l'autre état.
Calcul approché de la période du multivibrateur astable
On suppose que les tensions de seuil et de saturation sont nulles..
On prend comme origine des temps l'instant ou T1 se sature.
Si u(t) est la tension aux bornes de de C1 l'équation de sa charge à travers Rb2 et l'espace émetteur-collecteur de T1 qui est saturé est : Rb2.i(t) + u(t) = U.
i(t) = dQ(t) / dt = C1.du(t) / dt. On tire Rb2.C1.du(t) / dt = U. On pose τ1 = Rb2.C1.
L'équation générale est τ1.du(t) / dt +u(t) = U.
Les solutions générales et particulières sont
: u1(t) = A.e−t1 / τ et u2(t) = U.
En t = 0 u(0) = − U. Donc u(t) = U. { 1 − 2.e−t / τ1}.
Le système bascule quand u(t1) = VBE = 0
soit pour ½ = e−t1 / τ1 soit t1 ≈ 0,7 Rb2.C1.
On peut calculer de la même façon la durée de saturation de T2.
La période de l'astable est donc voisine de T = 0,7.( Rb2.C1 + Rb1.C2)
Cette valeur est approchée à cause des approximations réalisées.
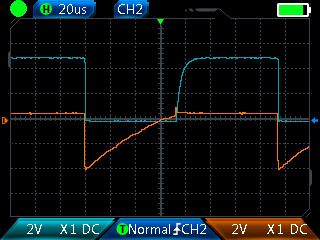 |
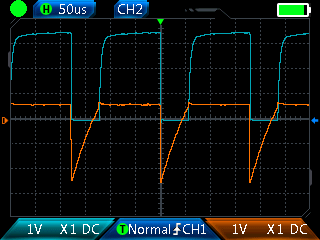 |
En bleu Vc1. En orange Vb2 |
U = 5 V. |
Exercices
1 ) Calculer les périodes pour les deux cas proposés et vérifier avec les oscillogrammes. Quel est l'aspect des diodes LED.
2) Mêmes questions si les données sont :
U = 5 V.
Rc1 = Rc2 = 330 Ω. Rb1 = Rb2 = 10 kΩ.
C1 = C2 = 100 µF
