Transistor amplificateur en mode émetteur commun.
On utilise un transistor BC108 avec β = 300 et Vbe = 0,67 V polarisé avec un pont de base et une résistance d'émetteur.
Consulter cette page pour avoir des informations complémentaires sur ce montage.

Polarisation du circuit.
On donne Vcc = 15 V, Rc = 2670 Ω, Re = 330 Ω.
Calculer Ic pour obtenir Vce = Vcc / 2 puis la valeur de Ib.
On impose un courant Ip = 1 mA dans le pont de base ( Ip >> Ib)
En déduire les valeurs des résistances R1 et R2.
Dans ce cas l'équation de la droite de charge est :
Vce = Vcc − (Rc + Re).Ic

Étude du circuit.
On applique le signal d'entrée sur la base par l'intermédiaire d'un condensateur de forte valeur pour que son impédance soit négligeable même pour la fréquence la plus faible utilisée.
On utilise le modèle du transistor en mode des petits signaux.
Rappels :
Les petites lettres i et v correspondent aux variations des courants et des tensions
Dans ce modèle on représente le transistor (cadre en pointillés) par sa résistance d'entrée h₁₁(Ω) ≈ 26.β / IC (en mA), un générateur de courant iC = h₂₁.iB = β.iB et par son admittance de sortie h₂₂ = iC / vCE.
On utilise souvent la pente du transistor s = β / h₁₁.

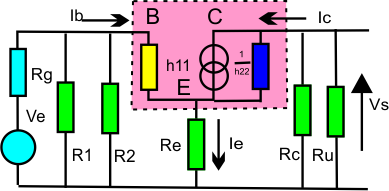Dans ce modèle le générateur d'alimentation et les condensateurs sont des courts-circuits pour les signaux variables.

Équations du circuit sans découplage.
Dans ce cas la pente de la droite de charge dynamique est Re.
ve = h₁₁.iB + Re.(iB + iC) ≈ (h₁₁ + β.Re).iB.
On considère la résistance h₂₂⁻¹ infinie.
vSM = − Rs.iC (avec Rs = Rc // Ru)
Av = vSM / ve = − Rs.β.iB / (h₁₁ + β.Re).iB.
Av = − Rc.β / (h₁₁ + β.Re).
Si la charge est infinie on a :
Av = − Rc / (h₁₁/ β + Re) ≈ − Rc / Re. (h₁₁ ≈ 3 kΩ)
Le gain en tension ne dépend du transistor utilisé. Le gain est négatif donc la tension de sortie est en opposition de phase avec la tension d'entrée.
Impédance d'entrée : Ze
Pour le transistor seul on a Z^T_E = h₁₁.iB + Re.β.iB >> h₁₁
Pour le montage Ze = Z^T_E // R1 // R2 ≈ 100 kΩ // R1 // R2
Impédance de sortie : Zs = Rc // Ru
Sur la maquette on a mesuré un gain en tension Av = − 7,6 (Rc / Re = 8.1)
Avec une charge Ru = 2,7 kΩ on mesure Av = − 3,7 : il est donc légitime de négliger l'effet de h₂₂⁻¹.

Conclusions : Le gain en tension est faible mais indépendant du transistor. L'impédance de sortie est de l'ordre de la résistance de collecteur. La résistance d'entrée est grande si les résistances du pont sont grandes mais alors le courant dans le pont n'est pas beaucoup plus grand que le courant de base Ib.

Équations du circuit avec découplage.
Pour supprimer l'effet de la contre-réaction d'émetteur sur le gain en régime variable, on place en parallèle sur la résistance d'émetteur un condensateur de forte valeur qui constitue un court-circuit pour les signaux variables avec le temps.
On considère que l'émetteur est à la masse.
On a : ve = h₁₁.iB et vs = − Zs.iC = − Zs.h₂₁.iB = − Zs.β.iB avec Zs = Rc // Ru.
Le gain en tension est Av = − Zs.β / h₁₁. Sans charge, le gain est donc Av = − Rc.β / h₁₁ = − s.Rc.
Sur la maquette on a mesuré un gain en tension Av = − 230.
La relation h₁₁(Ω) ≈ 26.β / IC (en mA) donne pour notre exemple h₁₁ = 26.300 / 2,5 = 3120 Ω.
Cela correspondrait à un gain de − 260.
Découplage partiel
On sépare la résistance d'émetteur en deux parties Re1 et Re2 et on place un condensateur aux bornes de la partie Re2 reliée à la masse. Le gain en tension devient Av ≈ − Rc / Re2 et la resistance d'entrée du transistor devient Z^T_E = h₁₁.iB + Re2.β.iB.
On obtient ainsi un gain plus important et une résistance d'entrée plus grande qu'avec une résistance d'émetteur totalement découplée.
Sur la maquette avec Re1 = 280 Ω et Re2 = 50 Ω on a mesuré un gain en tension Av = − 48. (Rc / Re2 = 54)

Conclusions : Le gain en tension est de l'ordre de β. L'impédance de sortie est de l'ordre de la résistance de collecteur. La résistance d'entrée toujours inférieure à h₁₁ est faible : Ce montage perturbe le fonctionnement de l'étage précédent.

Réponses : Ic = 2,5 mA Ib = 8,3 µA. R2 = 1,5 kΩ, R1 = 13,5 kΩ