On considère un pendule dont le moment d'inertie par rapport à son centre de gravité G est I_G = mR². (R est le rayon de giration du pendule). Le calcul du moment des forces par rapport à l'axe de rotation O permet d'établir l'équation du mouvement en fonction de l'angle d'inclinaison de OG = a par rapport à la verticale :

I_O d²θ/ dt² + mg.OG sin θ = 0.   (1)

D'après le théorème d'Huyghens sur les moments d'inertie, on peut écrire que I_O = I_G + ma² soit : I_O = m (a² + R²)
Si les amplitudes des oscillations sont assez faibles pour que l'on puisse confondre le sinus de l'angle avec l'angle, on peut intégrer l'équation et en déduire l'expression de la période qui est (2) :

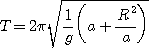
Il existe donc deux valeurs de a pour lesquelles la durée de la période d'oscillation est identique. (Pour le voir, élever l'expression de T au carré ce qui donne une équation du second degré en a).
Montrer que le produit a₁.a₂ = R² et que la somme a₁ + a₂ = gT² / 4.π² est la longueur du pendule simple équivalent au pendule composé.

---

Utilisation :
On peut au choix visualiser une animation du pendule ou la courbe T = f (OG) donnant la période en fonction de la distance OG = a.
Le rayon de giration R vaut 10 cm. Pour conserver un certain réalisme à l'animation, j'ai introduit un léger frottement visqueux (terme en dθ / dt) et fait une intégration numérique de l'équation du mouvement (Runge-Kutta à l'ordre 4).
Le point rouge correspond à la trace O de l'axe de rotation; le point vert à celle du centre de gravité G du pendule.
Les boutons [+] et [−] permettent de modifier la valeur de a entre 2,5 cm et 50 cm.
Il est possible de déterminer la période avec le chronomètre intégré.
L'amplitude initiale des oscillation est assez faible pour que l'expression de la période donnée par l'équation (2) soit correcte.