Dans cette méthode (dite de Rückhardt), on mesure la constante adiabatique d'un gaz en déterminant la période d'oscillation d'un piston qui coulisse dans un tube vertical relié à un récipient dont le volume est grand devant celui du tube.
Données numériques :
Rayon r du piston : 6 mm ;
Masse m du piston : 7,05g ;
Pression atmosphérique p : 105 Pa ;
Volume V du récipient : 1012 cm3
.
Equilibre statique :
La surpression introduite par le piston est :
Δp = m.g / π.r2 = 611 Pa.
Cette surpression est équivalente à 6 cm pour un manomètre à eau.
Oscillation :
Pour un déplacement x du piston, on peut écrire m.x" = π.r2Δp.x
Comme le processus est adiabatique, on a :
pVγ = Constante.
En différentiant, on tire Δpx = p.γ.ΔV / V.
L'équation du mouvement du piston est donc :
x" + γ.π2.r4p.x / m.V = 0 qui correspond à un mouvement harmonique dont la période est : 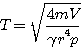
A cause des frottements, le mouvement du piston est de la forme : x = A e −bt. cos (ω.t)
On peut montrer que γ = Cp / cv = Mv2 / RT. (M = masse molaire du gaz, R constante des gaz parfaits = 8,82 J.mol-1.K-1).
Il est possible de déduire γ de la mesure de la vitesse du son dans le gaz.
Comparer avec la méthode de Clément-Desormes.
Utilisation :
Avec la souris, glissez le piston rouge dans le tube vertical en dehors de sa position d'équilibre (repérée par la flèche noire).
Cliquez sur le bouton [Départ] . On libère le piston et on déclenche le chronomètre.
Mesurer la durée d'une dizaine de période et en déduire la valeur de gamma pour le gaz contenu dans le récipient en utilisant la relation :
