On utilise un tube en U de section uniforme S rempli avec du mercure (masse volumique  m = 13,6 g/cm³).
Au repos, la hauteur du mercure dans chaque branche est égale à Z₀. La longueur de la branche horizontale du U est l = 20 cm.  La longueur de la colonne de mercure est donc égale à L = 2.Z₀ + l et sa masse m = μ.S.L

Oscillations d'un fluide :
On suppose que dans une branche le mercure se déplace de la hauteur x. La force de rappel est égale au poids d'une colonne de mercure de section S et de hauteur 2x.
Le principe fondamental de la dynamique permet d'écrire que :
m.d²x / dt² + 2.g.μ.S.x = 0, soit   μ.S.L.d²x / dt² + 2.g.μ.S.x = 0.
Le mouvement du mercure est donc un mouvement harmonique
x = A.cos(ω.t + φ) de période T_a = 2π.(L / 2.g)½
 (Noter que cette période est indépendante de la nature du fluide).

Détermination de gamma :
On ferme maintenant l'extrémité de la branche de droite du U avec un bouchon étanche.
Au repos, l'air isolé dans cette branche est à la pression atmosphérique P₀ et son volume est S.Y.
Si l'on met le mercure en oscillation (par exemple en appliquant avec une poire une impulsion de surpression dans la branche de gauche) la pression au dessus de la branche de gauche reste égale à P₀ tandis que celle dans la branche de droite est égale à P.
Cette fois la force de rappel vaut :  −2.g.μ.S.x − P.S + P₀.S
On admet que le phénomène est adiabatique et donc que : 
P₀(S.Y)^γ = P(S.[Y − x])^γ.
Si on se limite aux oscillations de faibles amplitudes, x reste petit devant Y; un développement au premier ordre permet d'écrire que :
P ≈ P₀(1 + γ.x / Y)
L'équation du mouvement est donc :
d²x / dt² + (2.g / L + γ.P₀ / μY.L ).x = 0.
La pression atmosphérique P₀ est équilibrée par une colonne de mercure de 76 cm de hauteur (conditions normales).
Le mouvement du mercure est un mouvement harmonique dont la période est :

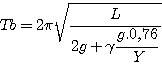
En mesurant les périodes d'oscillations T_a et T_b pour un même remplissage Z₀, on déduit la valeur de gamma :

γ = 2[T_a² / T_b² - 1].Y / 0,76.

Critique de la méthode :
La période des phénomènes est un peu trop grande pour avoir un réel adiabatisme.
Si la condition x << Y est remplie, il devient difficile de mesurer avec une bonne précision la valeur de la période.

---

Utilisation :
En cliquant sur le bouton [Départ] , on provoque l'oscillation du mercure.
Un chronomètre  affiche la valeur de t.
En glissant le curseur rouge avec la souris, on fait varier la valeur de Z₀ (et la période d'oscillation).
Déduire la valeur de gamma des valeurs affichées par le chronomètre.