Les valeurs du champ électrique et du potentiel crées par un ensemble de n charges ponctuelles qi sont données par :
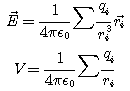
Le vecteur ri a pour origine la charge qi et comme extrémité le point étudié.
On considère ici 4 charges ponctuelles placées aux sommets d'un carré. On fait l'étude dans le plan contenant les charges en prenant comme origine le barycentre du carré et on place les charges sur les diagonales du carré.
Pour tracer les lignes de champ (courbes auxquelles est tangent le vecteur champ électrique), on part d'un point voisin d'une charge et on trace un petit segment dont l'orientation est celle du champ au point étudié et dont la longueur est proportionnelle à sa valeur. On répète le processus jusqu'à la sortie de l'épure.
Pour tracer les équipotentielles, on trace les courbes de niveau du potentiel.
Le système admet des symétries de révolution autour des médianes et des diagonales du carré et un axe tétragonal normal au plan.
Le champ à l'origine est nul. Comme le potentiel dérive du champ, le potentiel à l'origine est extremum. Montrer que c'est un minimum.
Sur l'axe Ox >0, il existe un autre point où le champ est nul, montrer que le potentiel en ce point présente un maximum. L'équipotentielle corrrespondante est tracée en blanc.
Dès que l'on s'éloigne des charges, les équipotentielles tendent vers des cercles centrés sur l'origine.
Comparer cette répartition de charges avec celle d'un quadrupôle (2 charges positives et deux charges négatives).
Utilisation :
Si l'on presse un bouton de la souris dans le cadre du dessin, et si l'on glisse la souris, on affiche avec des unités arbitraires les valeurs du champ et du potentiel au niveau du pointeur ainsi que le vecteur champ électrique.
On peut ainsi constater la décroissance rapide du champ quand on s'éloigne des charges (loi en 1 / r2).
Les lignes de champ électrique sont tracées en rouge. Les équipotentielles sont en bleu.
Bien noter que toutes les lignes de champ s'éloignent vers l'infini.
