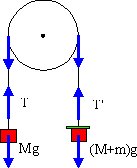
 On considère le système ci-contre (machine d'Atwood). On considère le système ci-contre (machine d'Atwood).
Deux masses identiques M sont reliées par un fil inextensible passant sur une poulie de rayon R et de moment d'inertie I.
A l'instant t initial, on place sur la masse de droite une surcharge m.
Comme les vitesses sont faibles, le frottement de l'air peut être négligé.
Les équations du système sont :
- T − M.g = M.γ (fil de gauche)
- (M + m).g − T' = (M + m).γ (fil de droite)
- I.d²θ / dt² = (T' − T).R (poulie)
Si I est négligeable, alors T = T' et γ = mg / (2M + m).
Ce dispositif permet l'étude de la chute des corps avec une valeur faible de l'accélération.
Utilisation :
Les cases à cocher permettent de modifier la valeur de la surcharge.
Toutes les 0,5 s le programme trace un marqueur donnant la position (en cm) de la masse de droite.
On suppose que les deux masses M valent 0,5 kg.
Vérifiez que le mouvement des deux masses est uniformément accéléré.
|