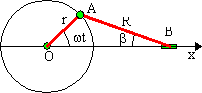
Une tige OA de longueur r tourne autour de O avec la vitesse constante ω.
Une tige AB permet de transformer le mouvement de rotation de A un en mouvement de translation. Elle est articulée en A et une glissière oblige le point B à rester sur Ox.
L'abscisse x de B est donnée par : x = r.cosω.t + R.cosβ
Sachant que dans le triangle OAB on a : r / sin(β) = R / sinωt, montrer que le mouvement de B est périodique mais qu'il n'est pas sinusoïdal.
Etudier le cas particulier R = r.
Utilisation :
L'animation permet d'observer le mouvement de rotation de A et le mouvement de translation de B.
Un curseur permet de faire varier le rapport K = R / r entre 1 et 5.
Un second curseur permet de faire varier la vitesse de l'animation.
Pour geler l'animation, cliquer sur le bouton droit de la souris. Relâcher ce bouton pour reprendre l'animation.
La courbe en bleu représente la courbe xB = f (t).
Si R est légèrement supérieur à r, les contraintes mécaniques sont très importantes.
Le système bielle-manivelle permet également de transformer un mouvement de translation en mouvement de rotation.