Dans cette page, on reprend l'étude de l'écoulement d'un liquide par un petit trou.
On considère un récipient cylindrique de rayon R₁ = 10 cm et de section S₁ percé par un petit trou de rayon R₂ et de section S₂ contenant un liquide non visqueux. Cette fois, le trou est réalisé sur la partie latérale du récipient.
Soit z la hauteur verticale entre le trou B et la surface du liquide A.
Lors de l'ouverture du trou la hauteur de liquide est z₀

La loi de conservation du volume du liquide implique que S₁.V₁ = S₂.V₂
On a : V₁ = − dz / dt
Si R₂ est beaucoup plus petit que R₁ la vitesse V₁ du fluide en A est négligeable devant V₂, vitesse du fluide en B le théorème de Bernouilli permet d'écrire que : P_A − P_B + μ.g.z = ½.μ.V₂².
Comme P_A = P_B (pression atmosphérique), il vient : V₂= (2.g.z)^½.
La vitesse d'écoulement est indépendante de la nature du liquide.
Comme la vitesse d'écoulement est fonction de z, elle n'est plus constante.
En écrivant la conservation du volume du fluide, on a : − S₁.dz = S₂.V₂.dt.
− dz / √h = √2g. S₂.dt. / S₁.
L'intégration de cette équation différentielle donne la loi de variation de la hauteur de liquide en fonction du temps.

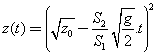
Mouvement du jet de liquide.
On néglige la résistance de l'air et la dispersion du jet.
Un élément dV du jet est soumis à son poids.
Sa vitesse initiale est horizontale et d'intensité V₂= (2.g.z)^½.
Les équations du mouvement sont donc : X = V_X.t = V₂.t et Y = ½.g. t².
Le mouvement est parabolique mais V_X diminue quand le vase se vide.
Si H est la hauteur du trou au-dessus du sol , montrer que la vitesse du jet quand il touche le sol est V₃ = [2.g.(z₀ + H)]^½.

Retrouver cette valeur en appliquant le théorème de Bernouilli entre la surface du liquide et le sol.

Dans l'application H = 40 cm