On peut définir l'ellipse comme le lieu des points dont la somme des distances à deux points fixes dits foyers est constante mais il existe d'autres définitions possibles.

Équation cartésienne.
L'équation cartésienne de l'ellipse est :
a est le demi-grand axe OA, b le demi-petit axe OB et c la demi-distance focale OF.
Si P est un point de l'ellipse, on a PF + PF' = 2.a
Sur la figure est tracé le cercle de rayon a et de centre O. On peut définir l'ellipse de centre O, de de demi-grand axe a et de demi-petit axe b par l'affinité d'axe Ox, de direction perpendiculaire à Ox et de rapport b / a.
L'aire de ce cercle étant π.a², l'aire de l'ellipse est π.ab.

Équation paramétrique.
Pour une ellipse dont les axes sont parallèles aux axes du repère, on peut paramétrer l'ellipse par :
x = a.cos(t) et y = b.sin(t) avec t ∈[0, 2π[.
Par contre le paramétrage x = a.cos(t) et y = b.sin(t + φ) correspond à une ellipse dont les axes ne sont plus parallèles à ceux du repère.
En physique les équations x = a.cos(t) et y = b.sin(t + φ) permettent la représentation de deux vibrations de même fréquence, orthogonales et déphasées de φ.

Équation polaire.
Dans le repère défini par le foyer et l'axe focal, l'équation polaire de l'ellipse de demi-axes a et b est :
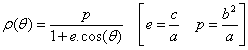e ∈]0, 1[ est l'excentricité (e = 0 correspond au cercle, e = 1 correspond à la parabole et e >1 à l'hyperbole).
p est le paramètre. C'est la valeur de ρ pour θ = π / 2 (axe en pointillés).

Tangentes à l'ellipse
Tangente en un point P (x0, y0) de l'ellipse :
De l'équation cartésienne, on déduit que la pente de la tangente en P à pour valeur α = ± b².x0 / a².y0.
Dans le cas de l'ellipse, il faut prendre la solution α = − b².x0 / a².y0.
La pente de la normale en P est β = − 1 / α.
La normale est la bissectrice interne de l'angle (FPF') alors que la tangente est la bissectrice externe.
Conséquence :
En optique un miroir elliptique est rigoureusement stigmatique pour ses foyers.
Cette propriété est aussi valable pour les ondes sonores.
Tangentes passant par un point M (x0, y0) extérieur à l'ellipse.
De l'équation cartésienne, on déduit que les pentes des tangentes à l'ellipse passant par M sont les solutions de l'équation :
α²(a² − x0²) + 2.α.x0.y0 + (b² − y0²) = 0.

Définition par un foyer et un cercle directeur.
On considère deux points F et F' distincts et un cercle de centre F et de rayon R = 2.a > FF'.
L'ellipse est l'ensemble des points P tels que P est le point du rayon FM satisfaisant à la condition PM = PF'.
P est situé à l'intersection du rayon FM et de la médiatrice de MF'.
Cette médiatrice est aussi tangente à l'ellipse en P.

Définition par un foyer et les directrices.
On choisit F tel que OF = c et une longueur a. Les directrices sont les droites x = ± a² / c.
On pose e = c / a et b tel que b² = a² − c².
La droite y = d (−b < d <b) coupe les directrices en H et H'.
P est le point de cette droite tel que PF = e.PH. L'ensemble des points P forme une ellipse d'axes 2.a et 2.b.
On peut vérifier que PF + e.PH' = 2.a = PF + PF'.
Fonctionnement d'une lentille elliptique :
Considérons la quantité PF + ePH'  comme un chemin optique. Si l'intérieur de l'ellipse est constitué d'un milieu d'indice n et l'extérieur d'indice e.n, les rayons incidents parallèles à l'axe de l'ellipse situés du côté de (D') seront réfractés en rayons passant tous par F.