On peut définir l'hyperbole comme l'ensemble des points dont la différence des distances à deux points fixes est constante mais il existe d'autres définitions possibles.

Équation cartésienne.
Dans le repère ou les coordonnées des foyers sont (± c, 0) l'équation cartésienne de l'ellipse est :

a est le demi-grand axe OA, b le demi-petit axe OB et c la demi-distance focale OF.
Si P est un point de l'ellipse, on a PF' − PF = 2.a
L'excentricité de l'hyperbole e = c / a est supérieure à 1.
L'hyperbole possède les asymptotes d'équations y = ± b.x / a

Équation paramétrique.
Pour une hyperbole dont les axes sont parallèles aux axes du repère, on peut paramétrer l'ellipse par :
x = a / cos(t) et y = b.tan(t) avec t ∈[0, 2π[.
La relation cosh²(t) − sinh²(t) = 1 conduit au paramétrage suivant :
x = ± cosh(t) et y = sinh(t) avec t ∈]−∞, ∞[.
Cette représentation est plus simple à utiliser.

Équation polaire.
Dans le repère défini par le foyer et l'axe focal, l'équation polaire de l'hyperbole de demi-axes a et b est :

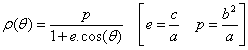
e >1 est l'excentricité (e = 0 correspond au cercle, e = 1 correspond à la parabole et e >1 à l'hyperbole).
p est le paramètre. C'est la valeur de ρ pour θ = π / 2 (axe en pointillés).

Tangentes à l'ellipse
Tangente en un point P (x0, y0) de l'ellipse :
De l'équation cartésienne, on déduit que la pente de la tangente en P à pour valeur α = ± b².x0 / a².y0.
Dans le cas de l'hyperbole, il faut prendre la solution α = b².x0 / a².y0.
La pente de la normale en P est β = − 1 / α.
La normale est la bissectrice interne de l'angle (FPF') alors que la tangente est la bissectrice externe.
Conséquence :
En optique un miroir hyperbolique est rigoureusement stigmatique pour ses foyers.

Tangentes passant par un point M (x0, y0) extérieur à l'ellipse.
De l'équation cartésienne, on déduit que les pentes des tangentes à l'ellipse passant par M sont les solutions de l'équation :
α²(a² − x0²) + 2.α.x0.y0 − (b² + y0²) = 0.

Définition par un foyer et un cercle directeur.
On considère deux points F et F' distincts et un cercle de centre F et de rayon R = 2.a < FF'.
L'hyperbole est l'ensemble des points P tels que P est le point du rayon FM satisfaisant à la condition PM = PF'.
P est situé à l'intersection du rayon FM et de la médiatrice de MF'.
Cette médiatrice est aussi tangente à l'hyperbole en P.

Définition par un foyer et les directrices.
On choisit F tel que OF = c et une longueur a. Les directrices sont les droites x = ± a² / c.
On pose e = c / a et b tel que b² = c² − a².
La droite y = d coupe les directrices en H et H'.
P est le point de cette droite tel que PF = e.PH. L'ensemble des points P forme une hyperbole d'axes 2.a et 2.b.
On peut vérifier que e.PH' − PH = 2.a .

Hyperbole équilatère
C'est une hyperbole dont les asymptotes sont orthogonales.
Le produit des pentes des asymptotes doit être égal à − 1 ce qui implique que a = b et e = c / a = 2^½.
Par rotation de π / 4 de cette hyperbole, on obtient une hyperbole d'équation Y = a² / 2.X.
Pour a = 2^½, on obtient la fonction inverse Y = 1 / X.