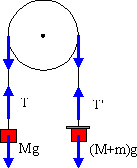
On considère dispositif ci-contre (machine d'Atwood) qui permet l'étude de la chute des corps avec une valeur faible de l'accélération.
Deux masses M identiques sont reliées par un fil inextensible passant sur une poulie de rayon R de masse Mp et de moment d'inertie I.
On néglige la masse du fil, les frottements et la résistance de l'air et on admet que le fil ne glisse pas sur la poulie.
Si ume masse s'élève de y, la poulie tourne d'un angle φ = y / R.
Si l'accélaration verticale d'une masse est γ, l'accélération angulaire de la poulie est :
d2φ / dt2 = α = γ / R
On place sur la masse de droite une surcharge m et on libère le système à l'instant t = 0.
Les équations du système sont :
I.α= (T' − T).R (Théorème du moment cinétique)
T − M.g = M.γ = Mα.R (fil de gauche)
T' − (M + m).g = (M + m).γ = (M + m)αR (fil de droite)
Dans la première équation, on remplace T et T' par leurs expressions . En tenant compte du fait que I = ½.Mp.R2, on tire :
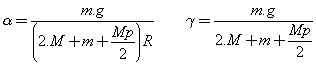
Utilisation :
Avec les sliders on peut modifier la valeur de la surcharge m et la masse de la poulie Mp.
On suppose que les deux masses M valent 0,5 kg.
On peut le rôle du moment d'inertie de la poulie.
Vérifiez que le mouvement des deux masses est uniformément accéléré.
En toute rigueur il faudrait tenir compte de la masse du fil qui n'est pas vraiment négligeable.
cf(http://res-nlp.univ-lemans.fr/NLP_E_M02_G01/co/NLP_E_M02_G01_02.html)