Pour étudier le mouvement d'une planète, on peut comme dans la page sur les forces centrales intégrer numériquement les équations différentielles du mouvement. On peut aussi utiliser les solutions analytiques déduites de la loi de Newton.

La troisième loi de Kepler dit que : T² / a³ = 4.π² / G.M
(G = 6,67428.10 ⁻¹¹ constante de gravitation et M valeur de la masse centrale).
Ici, pour vérifier que la période T de rotation reste constante si le demi grand axe de l'ellipse a reste constant, on a utilisé les solutions analytiques.
On compare les mouvements d'une masse m sur une orbite circulaire de rayon a et sur une orbite elliptique d'excentricité e variable. Dans le cas de l'orbite circulaire, le vecteur vitesse est toujours normal au rayon vecteur et sa norme est constante.

Notations utilisées :
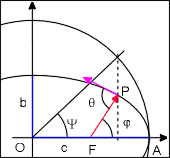O est le centre de l'ellipse.
A est le périapse*. OA = a.
F est le foyer de l'ellipse qui correspond au centre de gravité des masses M et m.
OF = c = a.e = (a² − b²)^½
FP = r est le rayon vecteur.
φ (angle AFP) est l'anomalie vraie.
ψ est l'anomalie excentrique.

Si les coordonnées de P sont x et y, ψ est l'angle tel que : x = a.cos(ψ) et y = b.sin(ψ).

Les anomalies vraie et excentrique sont reliées par la relation :
Enfin θ est l'angle entre le rayon vecteur r et le vecteur vitesse V.
Détermination de la position :
Pour calculer la position de m à l'instant t, on utilise l'équation du temps de Kepler : t = T.(ψ − e.sin(ψ)) / 2.π.

Pour chaque valeur de t, il faut résoudre numériquement cette équation transcendante pour calculer la valeur de ψ puis en déduire la valeur de φ puis les valeurs de x(t) et de y(t). Pour cette résolution, on peut utiliser par exemple une méthode de zéro.

Détermination de la vitesse :
Le vecteur vitesse est tangent à la trajectoire en P. On calcule r = |r| à partir de x(t) et de y(t).
La relation : b² / (r².sin²(θ)) − 2.a / r = − 1 permet de déterminer la valeur de θ à l'instant t.
On utilise la constance du moment cinétique L d'une force centrale pour calculer V : |V| = V = L / r.sin(θ)
On peut consulter par exemple ce document pour avoir la démonstration des formules utilisées.

Utilisation :
Utiliser le slider pour modifier la valeur de l'excentricité. Le traitvert vertical permet de visualiser les écarts entre les progressions de P sur les deux types d'orbites.

* Le point opposé du grand axe est l'apoapse. Dans le cas de la Terre ces points se nomment périgée et apogée.