Un anneau circulaire de rayon a porte une charge Q répartie uniformement. On étudie le potentiel et le champ électrique en un point M situé sur l'axe de l'anneau.

Dans le cas de charges ponctuelles, on rappelle que :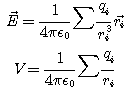

Potentiel en M
On pose K = 1 / 4πε₀ et x = M. Toutes les charges sont à la même distance PM du point M.

V(M) = K.Q / (x² + a²)½

Champ électrique en M
Un élement dl de l'anneau entourant le point P porte une charge dq = λ.dl avec λ = Q / 2π.a.
Cet élement crée en M, un champ dE = K.λ.dl / (x² + a²).
Le système est de révolution donc la résultante des champs élémentaires est porté par Ox.
La composante de dE selon Ox est dE = K.λ.dl.cos(α) / (x² + a²).
Soit dE = K.λ.dl.x / (x² + a²)^3/2.
L'intégration est immédiate.

E(M) = K.Q.x / ( x² + a² )^3/2

Exercices
* Vérifier que l'on a bien E = − dV / dx

* Montrer que pour x = ± a / √2, le champ présente un maximun et que la courbe du potentiel présente un point d'inflexion.

* Comparer ces résultats avec ceux du disque chargé.