Un disque porte une densité de charge uniforme σ. On étudie le potentiel et le champ électrique en un point M situé sur l'axe de l'anneau.

Dans le cas de charges ponctuelles, on rappelle que :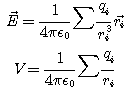

Potentiel en M
On pose K = 1 / 4πε₀ et x = M.
On a dV = K.dq / r.
On considère la couronne comprise entre les cercles de rayons r et r + dr de surface dS = 2π.r.dr.
Cette couronne porte la charge dq = σ.dS = 2π.σ.r.dr et tous les point de la couronne sont à la distance (x² + r²)½ de M.
dV = (σ / 4ε₀).2.r.dr / (x² + r²)½ .
En intégrant entre 0 et a, on tire

V(M) = (σ /2ε₀).[ (x² + a²)½ − |x| ]

Le potentiel est nul à l'infini

Champ électrique en M
Par raison de symétrie, le champ est orienté selon OM et sa valeur est donnée par la relation E = − ∂V / ∂x.

Pour x > 0, on tire E(M) = (σ / 2ε₀)[1 − x / (x² + a²)½]

Pour x < 0, on tire E(M) = − (σ / 2ε₀)[1 + x / (x² + a²)½]

Comparer ces résultats avec ceux de l'anneau chargé.