Théorie des orbitales moléculaires : cas d'un complexe octaédrique
Le diagramme d'énergie des orbitales moléculaires (O.M.) est construit par recouvrement des orbitales atomiques (O.A.) des ligands et du métal de transition. Dans le cas d'un complexe octaédrique des métaux de la 1ère série de transition, il y a 9 orbitales de valence pour l'ion métallique : les orbitales (3d, 4s, 4p) ou (4s, 4p, 4d) .
6 de ces O.A. : ${{\text{d}}_{{{\text{x}}^{\text{2}}}-{{\text{y}}^{\text{2}}}}}\text{, }{{\text{d}}_{{{\text{z}}^{\text{2}}}}}\text{, s, }{{\text{p}}_{\text{x}}}\text{, }{{\text{p}}_{\text{y}}}\text{, }{{\text{p}}_{\text{z}}}$
ont leur lobes orientés suivant les axes Ox, Oy et Oz c'est à dire dans les directions des liaisons Métal-Ligand et par suite conduiront à des liaisons de type $\text{ }\!\!\sigma\!\!\text{ }$ .
3 de ces O.A. : ${{\text{d}}_{\text{xy}}}\text{, }{{\text{d}}_{\text{xz}}}\text{, }{{\text{d}}_{\text{yz}}}$ sont au contraire orientées pour l'établissement de liaisons $\text{ }\!\!\pi\!\!\text{ }$ ou bien ne forment pas de liaisons.
Chacun des 6 ligands doit disposer d'une orbitale de type $\text{ }\!\!\sigma\!\!\text{ }$. Ces 6 O.A. individuelles sont alors combinées linéairement pour obtenir 6 O.A. hybrides. Par recouvrement des ces 6 O.A. hybrides avec les 6 O.A. de M, on forme les 6 liaisons ${{\text{ }\!\!\sigma\!\!\text{ }}_{\text{M-L}}}$ . On obtient ainsi les orbitales moléculaires liantes et antiliantes.
Si le ligand possède des orbitales $\text{ }\!\!\pi\!\!\text{ }$ , on les combine linéairement pour obtenir des orbitales hybrides pouvant se recouvrir avec les O.A. $\text{ }\!\!\pi\!\!\text{ }$ de M. De même, on obtient des O.M. liantes et antiliantes de type $\text{ }\!\!\pi\!\!\text{ }$.
Cas de ${{\left[ \text{Ti}{{\left( {{\text{H}}_{\text{2}}}\text{O} \right)}_{\text{6}}} \right]}^{\text{3+}}}$ : formation de liaisons $\text{ }\!\!\sigma\!\!\text{ }$
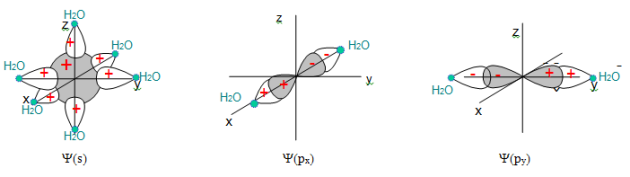
L'atome de titane dispose de ses orbitales de valence 3d, 4s et 4p. Chaque molécule d'eau fournit une orbitale de valence de type ${{\sigma }_{\text{s}{{\text{p}}^{\text{3}}}}}$. La combinaison des orbitales $\sigma $ de H2O avec l'orbitale 4s du cation conduit à une O.M. liante : $\text{ }\!\!\Psi\!\!\text{ }\left( \text{s} \right)\text{ = }{{\text{C}}_{\text{1}}}\left( \text{4s} \right)\text{+ }{{\text{C}}_{\text{2}}}\text{(}{{\text{ }\!\!\sigma\!\!\text{ }}_{\text{1}}}\text{+}{{\text{ }\!\!\sigma\!\!\text{ }}_{\text{2}}}\text{+}{{\text{ }\!\!\sigma\!\!\text{ }}_{\text{3}}}\text{+}{{\text{ }\!\!\sigma\!\!\text{ }}_{\text{4}}}\text{+}{{\text{ }\!\!\sigma\!\!\text{ }}_{\text{5}}}\text{+}{{\text{ }\!\!\sigma\!\!\text{ }}_{\text{6}}}\text{)}$ Les autres orbitales moléculaires sont obtenues en combinant successivement les 5 O.A. restantes de $\text{T}{{\text{i}}^{\text{3+}}}$ avec celles des ligands qui se trouvent dans leurs directions. On obtient ainsi : $\Psi ({{p}_{x}})={{C}_{3}}(4{{p}_{x}})+{{C}_{4}}({{\sigma }_{4}}-{{\sigma }_{2}})$ $\Psi \text{(}{{\text{p}}_{\text{y}}}\text{)}={{\text{C}}_{\text{3}}}\text{(4}{{\text{p}}_{\text{y}}}\text{)}+{{\text{C}}_{\text{4}}}\text{(}{{\sigma }_{3}}-{{\sigma }_{\text{5}}}\text{)}$ $\Psi \text{(}{{\text{p}}_{\text{z}}}\text{)}={{\text{C}}_{\text{3}}}\text{(4}{{\text{p}}_{\text{z}}}\text{)}+{{\text{C}}_{\text{4}}}\text{(}{{\sigma }_{1}}-{{\sigma }_{\text{6}}}\text{)}$ $\Psi \text{(}{{\sigma }_{{{x}^{2}}-{{y}^{2}}}}\text{)}={{\text{C}}_{\text{5}}}\text{(3}{{\text{d}}_{{{x}^{2}}-{{y}^{2}}}}\text{)}+{{\text{C}}_{\text{6}}}\text{(}{{\sigma }_{\text{4}}}+{{\sigma }_{\text{2}}}-{{\sigma }_{\text{5}}}-{{\sigma }_{\text{3}}}\text{)}$ $\Psi \text{(}{{\sigma }_{\text{z}}}^{\text{2}}\text{)}={{\text{C}}_{\text{7}}}\text{(3}{{\text{d}}_{\text{z}}}^{\text{2}}\text{)}+{{\text{C}}_{\text{8}}}\text{(2}{{\sigma }_{\text{1}}}+\text{2}{{\sigma }_{\text{6}}}-{{\sigma }_{\text{4}}}-{{\sigma }_{\text{3}}}-{{\sigma }_{\text{2}}}-{{\sigma }_{\text{5}}}\text{)}$ Les fonctions antiliantes correspondantes s'obtiennent en changeant le signe + par le signe -. | 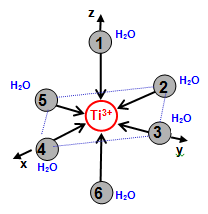 |
Ci-dessous sont représentés les recouvrements des orbitales atomiques qui conduisent aux orbitales moléculaires liantes :

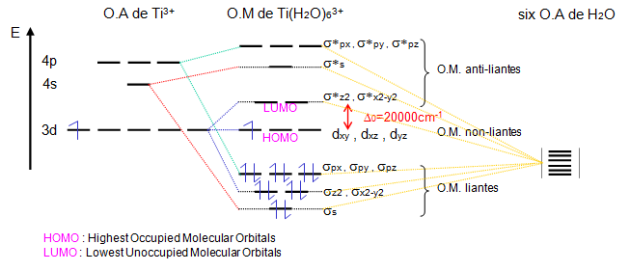
Le diagramme d'énergie des orbitales moléculaires de ${{\left[ \text{Ti}{{\left( {{\text{H}}_{\text{2}}}\text{O} \right)}_{\text{6}}} \right]}^{\text{3+}}}$ est présenté ci-dessous .
Les six paires d'électrons apportés par les ligands et l'électron de l'ion $\text{T}{{\text{i}}^{\text{3+}}}$ occupent les OM de plus basse énergie. Le dernier niveau occupé (HOMO) correspond à une orbitale moléculaire triplement dégénérée de type ${{\text{t}}_{\text{2g}}}$ alors que le premier niveau non occupé (LUMO) correspond à une orbitale moléculaire doublement dégénérée de type ${{\text{e}}_{\text{g}}}$ .
On comprend facilement que l'absorption d'une énergie lumineuse adéquate ($\text{ }\!\!\Delta\!\!\text{ E}$) permettra de faire passer un électron de l'orbitale moléculaire HOMO à l'orbitale moléculaire LUMO. Ce résultat est tout à fait identique à celui observé dans la théorie du champ cristallin, seule la nature de la liaison est changée.
Fondamental :
La théorie des OM permet d'expliquer la couleur des complexes d'éléments d et la modification des propriétés magnétiques en relation avec la différence d'énergie $\text{ }\!\!\Delta\!\!\text{ E}$ entre les niveaux des orbitales moléculaires HOMO et LUMO.