Retour

La structure cristalline des solides inorganiques
Les notions fondamentales - Les empilements de sphères

1. Pourquoi étudier les solides ?

2. Quelques notions de base sur la périodicité

• réseau (modes de réseau)
• motif (noeud)
• structure cristalline
• maille (contenu d'une maille)
• coordonnées réduites
• indice de coordination - coordinence

3. Représentation des structures

• Perspective
• Projection (dans un plan), diagrammess

4. Empilement compact de sphères

• empilement hexagonal compact (hcp)
• empilement cubique compact (ccp ou cfc)

5. Structures des métaux

6. Les sites intersticiels dans les empilements compacts

Pourquoi étudier les solides ?

1. Tous les composés sont solides sous certaines conditions de température et de pression..

     Certains n'existent qu'à l'état solide

Propriétés mécaniques

• Métaux/Alliages, e.g. Titane pour les avions
• Ciment/Matériaux Ca₃SiO₅
• Céramiques, e.g.argiles , BN, SiC
• Lubrifiants, e.g. Graphite, MoS₂
• Abrasifs, e.g. Diamant, Quartz( SiO₂)

  Propriétés électriques

• Conducteurs métalliques, e.g. Cu, Ag...
• Semiconducteurs, e.g. Si, GaAs
• Supraconducteurs, e.g. Nb₃ Sn, YBa₂ Cu₃ O₇
• Electrolytes, e.g. LiI pour les batteries de pacemakers
• Piézoelectriques, e.g.a -Quartz ( SiO₂) in watches

  Propriétés magnétiques

• e.g.CrO₂, Fe₃O₄ pour les technologies d'enregistrement (audio, video)

  Propriétés optiques

• Pigments, e.g.TiO₂ dans les peintures
• Phosphors, e.g. Eu³⁺ dans Y₂O₃ est rouge pour la TV
• Lasers, e.g. Cr³⁺ dans Al₂O₃ c'est le rubis
• Doublage de fréquence, e.g. LiNbO₃

  Catalyseurs

• Zéolites ZSM-5 (un aluminosilicate)
  - raffinage du pétrole
  - méthanol octane
  
  

  Senseurs

• Senseur à Oxygène, e.g. Solution solide ZrO₂/CaO

3. Les solides (surtout les monocristaux) ont toujours fasciné.

Quelques repères historiques
(X-date = depuis la découverte de la diffraction des rayons X - 1912) - BX = avant - AX = Après -)

Date	X-Date	Evènement
ca. 6000 BC		Les égyptiens extraient la turquoise
Antiquité		Les gemmes (particulièrement diamant, saphir, émeraude & rubis) sont très appréciés
400 BC	ca. 2310 BX	Théophraste décrit la forme régulière des cristaux de grenats
64 BC	1976 BX	Strabo nomme Quartz krystlloz (crystallum en Latin), en fait notre 'cristal'
1597	315 BX	L'alchimiste Libavius constate que la forme géométrique des cristaux est caractéristique des sels concernés.
17ème S	ca. 302 BX	Boyle, Leeuwenhoek, Kepler, Hooke... font de nombreuses observations avec le microscope récemment inventé
1611	301 BX	Kepler suggère que la symétrie hexagonale des flocons de neige est due à un empilement régulier des particules les constituant"
1665	247 BX	Hooke suggère que les cristaux sont composés de "spheroïdes"
1669	243 BX	Steno observe que les cristaux de Quartz ,quelle que soit leur origine montrent les mêmes angles interfaciaux caractéristiques.
1780	132 BX	Carangeot invente le Goniomètre par contact- il mesure les angles interfaciaux permettant d'accéder à un grand nombre de données cristallographiques.
1783	129 BX	Les études de Bergman sur le clivage des cristaux (sans doute de la calcite) lui suggère que le cristal est formé d'unités rhomboèdriques empilées.
1783	129 BX	de l'Isle formule la loi de constance des angles entre les faces.
1801	111 BX	Haüy introduit la loi des 'indices rationnels' Les lois fondamentales de la morphologie cristalline sont établies.
1808	104 BX	Malus constate la polarisation de la lumière par certains cristaux
1809	103 BX	Wollaston invente le goniomètre par réflexion. Ceci conduit à une très grande amélioration de la précision sur les données angulaires.
1815	97 BX	Biot découvre les formes levo- et dextro-gyres du Quartz
1819-22	93 BX	Mitscherlich découvre : l'Isomorphisme (des cristals de différentes compositions peuvent avoir la même forme) le Polymorphisme (des cristaux de formes différentes peuvent avoir la même composition) [= Allotropie]
1839	73 BX	Miller utilise les Indices de Miller pour désigner les faces du cristal
1848	64 BX	Pasteur découvre les cristaux énantiomorphes
1880s-90s	32 BX	Sohncke, Federov, Schönfleiß & Barlow développent la théorie de la symétrie interne cristalline - mais ne dispose pas de faits expérimentaux pour valider leurs théories
1906-19	6 BX	"Chemische Krystallographie" de Groth tabule les propriétés morphologiques, optiques et autres de 7000 substances cristallisées (pas d'information sur la structure interne - pas de techniques expérimentales).
1907	5 BX	Barlow & Pop proposent que dans un cristal les ions se comportent comme des sphères dures en contact.
1912		Friedrich, Knipping & von Laue découvrent la diffraction des rayons X
1913	1 AX	W.H. & W.L. Bragg utilisent la dépendance en orientation de la diffraction des rayons X d'un monocristal pour résoudre la structure de NaCl (& ensuite diamant etc...)
1913	1 AX	Ewald introduit le concept du Réseau Réciproque
1914	2 AX	Théorie de Debye de l'agitation thermique des atomes dans un solide (et donc le facteur Debye-Waller dans les structures cristallines )
1916	4 AX	Expériences de Debye & Scherrer de diffraction des poudres
1924	12 AX	Bernal et al. - structure du Graphite
1926	14 AX	Défauts de structures étudiés par Frenkel
1926	14 AX	Formulation de l'atome sphérique par Goldschmidt
1927	15 AX	Reprise du Model ionique de Goldschmidt par Pauling dans les règles de Pauling
1929	17 AX	Générateur de rayons X à anode tournante - autorise des intensités du rayonnement X plus fortes pour de meilleurs clichgés de diffraction.
1934	22 AX	Fonction de Patterson pour résoudre la structure par diffraction des rayons X
1934	22 AX	Ruska prend des images avec le premier microscope électronique à transmission.
1936	24 AX	Halaban & Preiswerk -diffraction des neutrons par un cristal
1941	29 AX	Hughes utilise l'affinement par moindres-carrés pour obtenir le meilleur résultat possible à partir d'un jeu de données de diffraction.
1944	32 AX	Buerger invente la chambre de précession
1948	36 AX	Harker & Kasper - Méthodes directes pour la résolution de la structure à partir de données de diffraction X.
1950s	ca. 38 AX	Les diffractomètres automatiques et les ordinateurs facilitent considérablement la détermination des structures cristallines.
1951	39 AX	Bijvoet utilise la diffusion anomale pour déterminer la chiralité (configuration absolue)
mi - 1950	ca. 43 AX	Premières utilisations des ordinateurs pour résoudre des structures cristallines.
1955	43 AX	Principes de Laves - remplissage de l'espace dans les cristaux
1956	44 AX	Menter obtient la première image d'un réseau par microscopie électronique à transmission (TEM).
1957	45 AX	Müller - La microscopie d'émission de champ permet de visualiser des atomes dans un métal.
1970	58 AX	Crewe, Wall et Langmore - Microscopie électronique à balyage en champ sombre (première méthode pour imager les atomes lourds individuellement)
1971	59 AX	Formanek et al. - Première détection d'un atome isolé en microscopie électronique à transmission à haute résolution(HREM)
1974	62 AX	Iijima - première observation de défauts ponctuels dans des structures par microscopie électronique
1980s	ca. 68 AX	Rayonnement Synchrotron disponible - augmentation énorme de l'intensité des rayons X (clichés de Laue obtenus en quelques ms)
1982	70 AX	Détecteurs de rayons X bidimensionnels (gain de temps important pour la réalisation des clichés de diffraction X)
1982	70 AX	Binnig & Rohrer - Microscope à balayage à effet tunnel (STM) permet d'imager aussi les atomes légers en surface
1984	72 AX	Schechtman et al. découvrent les quasi-cristaux
198?	7? AX	Binnig et al. - La Microscopie à force atomique (AFM) permet d'obtenir des images des surfaces (souvent plus pratique que le STM)
1990	ca. 80 AX	Les données (coordonnées internes) de >200,000 structures cristallines sont enregistrées dans des bases de données.

Quelques notions de base sur la périodicité

RESEAU = Un ensemble infini de noeud (points) dans l'espace, chaque noeud (point) a le même environnement que ses voisins.

STRUCTURE CRISTALLINE = L'arrangement périodique des atomes dans le cristal. Il peut être décrit en associant à chaque noeud du réseau un groupe d'atomes appelé le MOTIF.

MAILLE = C'est le plus petit élément du cristal qui, répété par des translations successives reproduit le cristal entier.

Ne confondez pas les atomes avec les noeuds du réseau Les atomes sont des objets physiques (réels) alors que les noeuds sont des objets symboliques (virtuels) Les noeuds ne coïncident pas forcément avec le centre d'un atome. La maille primitive P contient seulement un noeud

RESEAUX 2D :   Exemple d'une couche dans la structure du GRAPHITE

Décompte des noeuds et des atomes Maille Primitive (1 noeud) mais le Motif est formé de 2 atomes de carbone Les atomes aux coins de la maille ne contribuent que pour 1/4 pour cette maille Les atomes sur les côtés de la maille 2D contribuent pour 1/2 dans cette maille Les atomes à l'intérieur de la maille 2D contribuent seulement dans cette maille

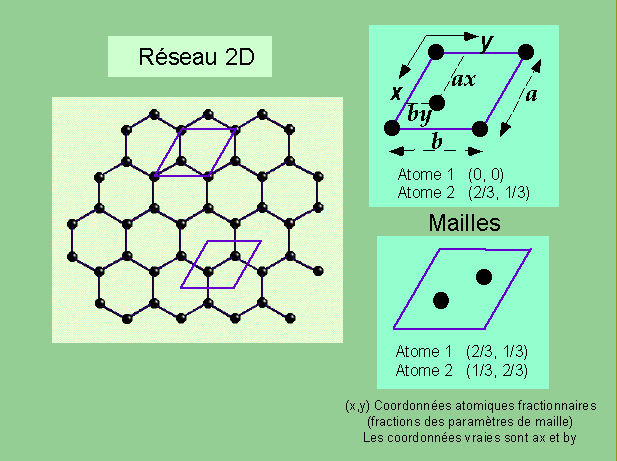Etude d'un solide 3D : le Graphite
C'est un arrangement en zigzag de couches hexagonales

Décompte des atomes Selon sa position dans la maille, un atome participe de manière différente dans la maille étudiée Un atome sur un sommet est commun à 8 mailles         ® 1/8 atome par maille Un atome sur une arête est partagé par 4 mailles        ® 1/4 atome par maille Un atome sur une face est partagée par 2 mailles         ® 1/2 atome par maille Un atome à l'intérieur 1 maille        ® 1 atome par maille

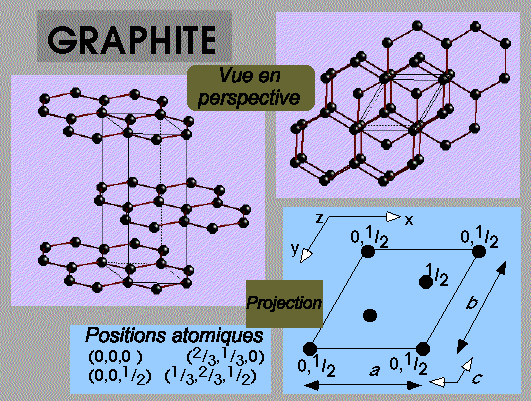Les 14 réseaux de BRAVAIS

La combinaison des 7 systèmes cristallins avec les modes de réseaux possibles conduit aux 14 réseaux 3D de Bravais

La combinaison de tous les éléments de symétrie dans les 14 réseaux de Bravais &emdash;> 230 groupes spatiaux

1926 -  Goldschmidt :
les atomes doivent être considérés comme des sphères dures.

Empilement compact de sphères

• Nombre de coordination = 12
• 74% de l'espace est occupé
• Les sites intersticiels les plus grands sont :-
  • octaédrique ( r = 0.414 R) ~ 1 par sphère
  • tétraédrique (r = 0.225 R) ~ 2 par sphère

     

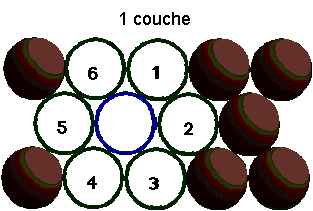
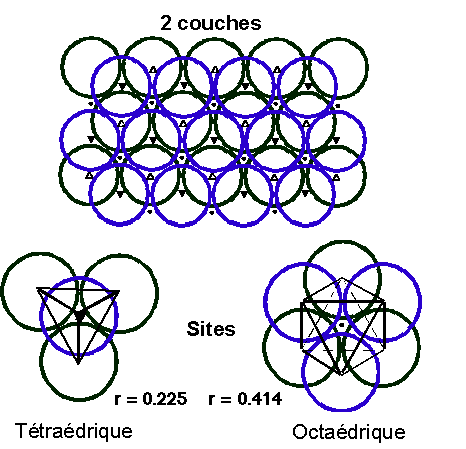
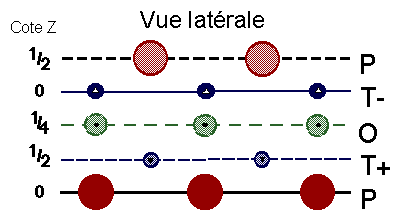
Les structures compactes les plus connues sont celles des métaux

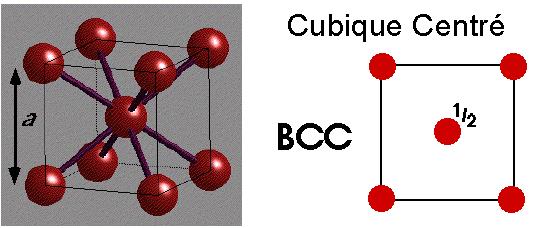
Une structure semi-compacte adoptée par certains métaux

68% de l'espace est occupé Nombre de coordination ? 8 Premiers voisins à 0.87a 6 Seconds voisins à a

• Ils ne sont pas tous en empilement compact
• Pourquoi des structures différentes ? sans doute lié à des effets secondaires tels que la direction des orbitales atomiques
• Il est difficile de prévoir la structure
  mais la structure cubique I est généralement adoptée dans le cas d'un faible nombre d'électrons de valence et en cas de polymorphisme, à plus haute température.

Les sites intersticiels dans les empilements compacts

Retour

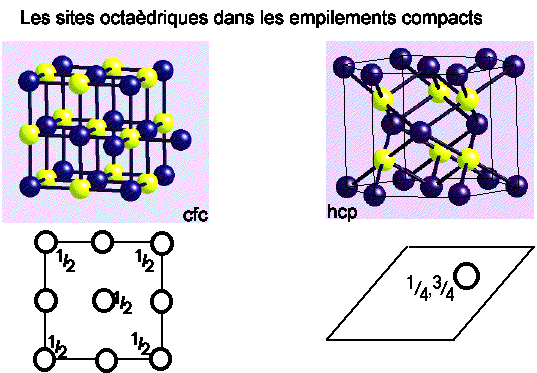
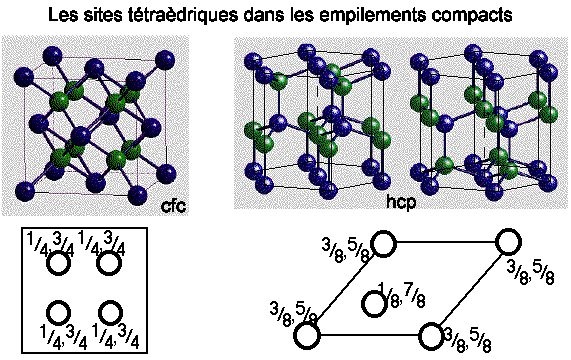
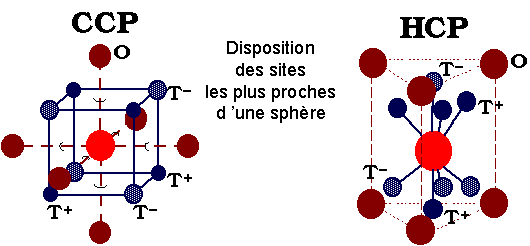
Lecture 2 - Lecture 3 - Lecture 4

© S.J.Heyes , Oxford, 1996                            Traduction -Adaptation : C. Jacoboni, Le Mans, 1998

Dernière mise à jour : 14/07/02