Miroirs plans
Le miroir plan
Un miroir plan est est une surface plane réfléchissante.
Image d'une source ponctuelle
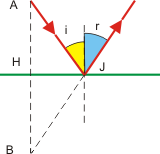 |
Un point source A émet un rayon qui frappe le miroir en J avec l'incidence i.
L'image d'une source ponctuelle dans un miroir plan est son symétrie par rapport au miroir.
|
Tous les rayons issus de A semblent après réflexion provenir de B : Le miroir plan est stigmatique.
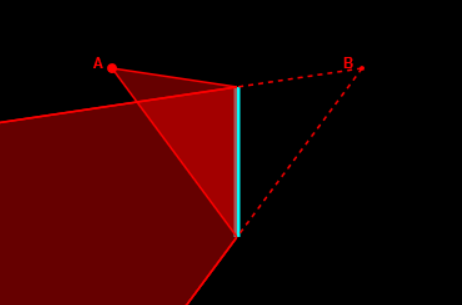
Image d'une source étendue
On peut considérer une source étendue comme la juxtaposition de ses points. Chacun d'eux donne une image dans le miroir. L'image de la source est la juxtaposition des ces points images.
L'image est le symétrique
de l'objet dans le miroir (symétrie par rapport à un plan).
Objet et image ne sont pas superposables sauf si l'objet présente un plan de symétrie. Ainsi l'image d'un trièdre direct est un trièdre inverse et l'image d'une main droite est une main gauche.
Il faut un nombre pair de réflexions pour obtenir des images superposables.
Réalisation des miroirs
Le pouvoir réflecteur d'un milieu correspond au rapport entre le flux réfléchi et le flux incident. Ce rapport est fonction du milieu incident et de la nature du miroir. Dans le cas ou le milieu incident est l'air, on distingue deux types de surfaces réfléchissantes.
Milieux transparents réfringents
Sous incidence normale, ces substances présentent un pouvoir réflecteur très faible.
On démontre à partir des formules de Fresnel que pour une incidence nulle, le pouvoir réflecteur est R = (N − 1)² / (N + 1)².
Ainsi pour un dioptre air-verre, le pouvoir réflecteur est de l'ordre de 4 % et pour un dioptre air-eau il vaut 2 %.
Le pouvoir réflecteur augmente avec l'angle d'incidence et tend vers 1 pour i = 90°.
Milieux à réflexion métallique
Pour ces matériaux, le facteur de réflexion est déjà élevé pour une incidence nulle et tend vers 1 pour l'incidence rasante. Les miroirs usuels sont réalisés par un dépôt d'argent obtenu par voie chimique sur une glace en verre.
Comme l'argent s'oxyde, on fait le dépôt sur la face arrière de la glace et on protège le dépôt avec un vernis.
Cette méthode fait qu'il y a aussi réflexion et réfraction vitreuse sur la face avant de la glace ce qui donne des images multiples.
Les miroirs de qualité sont réalisés par évaporation sous vide d'aluminium sur un support en verre. En agissant sur l'épaisseur de dépôt, il est possible de contrôler le facteur de réflexion et d'obtenir des miroirs semi-transparents.
Couches minces
Par évaporation sous vide, il est possible de déposer des couches successives de substances d'indices différents. Dans ces couches, se produisent des phénomènes d'interférences qui permettent d'obtenir des résultats variés : couche antireflets, lame semi-transparentes, filtres.
Rotation d'un miroir plan
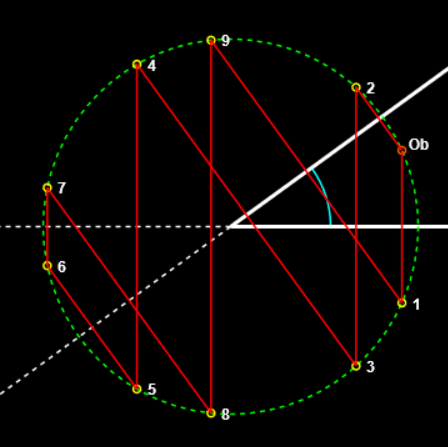
On considère un point source A et un miroir plan M tournant autour d'un axe vertical Oz.
La figure est tracée dans le plan normal à M contenant A.
L'axe Ox correspond à la position initiale du miroir (angle de rotation α
nul).
Dans ce cas, l'image (virtuelle) de A dans le miroir M est le point C symétrique de A par rapport à Ox.
Si l'angle entre OA et Ox est égal à β alors l'angle entre OC et Ox est aussi égal à β.
On fait tourner le miroir M d'un angle α autour de l'axe Oz.
B image de A dans le miroir est symétrique de A par rapport à la nouvelle position du miroir.
Elle est située sur le cercle de centre O et de rayon OA.
L'angle AOB devient égal à 2.(α + β).
Quand le miroir tourne d'un angle α autour d'un axe situé dans son plan, l'image d'un point fixe tourne autour du même axe d'un angle 2α.
Pour déplacer le point source, glisser le point jaune du curseur du haut avec la souris. Pour faire tourner le miroir, glisser le point rouge du curseur du bas avec la souris. Vérifier que la valeur de l'arc COB (tracé en jaune) est bien égale à 2α
Associations de miroirs plans
Deux miroirs
 |
Miroirs inclinés d'un angle α.
On considère deux miroirs plans normaux au plan de figure faisant entre eux l'angle α.
Pour plus de détails consulter cette page. |
Cas α = 90°.
Pour cette situation, il y a confusion des images I3 et I4. C'est un moyen pour orienter précisément deux
miroirs à 90°.
On peut constater que dans ce cas, un rayon émergeant ayant subi deux réflexions est parallèle au rayon incident.
Cas α = 45°. Un rayon après réflexion sur les deux miroirs est orthogonal au rayon incident.
Applications :
Redressement des images : Dans une lunette terrestre, l'image est inversée. On peut la redresser au moyen de deux systèmes de
miroirs orthogonaux. On préfère utiliser deux prismes rectangles isocèles attaqués par la face hypoténuse. Il y a réflexion totale
sur les faces latérales qui n'ont pas besoin d'être argentées. C'est le montage retenu dans les jumelles de vision.
Équerre optique : Si l'angle des miroirs est 45°, l'émergeant est à 90° de l'incident. Ici encore on préfère utiliser un prisme d'angle au sommet 45° dont les faces latérales sont argentées.
Kaléidoscope : Du grec "kalos" (beau), "eidos" (aspect) et skopien (observer). C'est un dispositif inventé en 1816 par BREWSTER utilisé maintenant comme jouet. Dans un tube constitué par trois miroirs verticaux formant un triangle équilatéral sont placés des objets colorés. La lumière pénètre par une extrémité et on observe par l'autre les réflexions multiples.
Miroirs parallèles
On considère deux miroirs parallèles et normaux au plan de figure.
Chaque miroir donne d'un objet une image virtuelle symétrique de celui-ci.
Chacune de ces images sert d'objet virtuel pour chaque miroir qui en donne une image symétrique.
On obtient une double infinité d'images.
Trois miroirs orthogonaux
Pour une étude complète de ce cas consulter cette page.

On considère trois miroirs plans orthogonaux M1 (bleuté, plan x = 0), M2 (orangé, plan y = 0) et M3 (vert, plan z = 0).
On envoie un rayon sur le point B du plan M3. Les cosinus directeurs du rayon incident sont cosα, cosβ et cosγ.
S'il se produit une suite de réflexions sur les trois miroirs alors le rayon émergent est parallèle au rayon incident.
Lors d'une réflexion sur un miroir plan, le rayon réfléchi est symétrique du rayon incident par rapport au plan du miroir.
Si les cosinus directeurs du rayon incident sont
cosα, cosβ et cosγ, les cosinus directeurs du rayon réfléchi par le miroir M3 sont cosα, cosβ et −cosγ.
Après une réflexion sur M2, les cosinus directeurs du rayon sont cosα, −cosβ et −cosγ.
Enfin après une troisième réflexion sur M1, les cosinus directeurs du rayon émergent sont : −cosα, −cosβ et −cosγ.
La direction du rayon émergent est opposée à celle du rayon incident.
On peut aussi utiliser la démonstration suivante :
Soient u et u' les vecteurs unitaires selon la direction des rayons incident et réfléchi par un miroir, n et t les vecteurs unitaires normaux et tangentiels du miroir dans le plan d'incidence et i l'angle d'incidence. On a :
u = sini.t − cosi.n et u' = sini.t + cosi.n ⇒ u' − u = 2.cosi.n = − 2.(s).n ⇒ u' = u − 2.(u.n).n
Soient n1, n2 et n3 les vecteurs unitaires normaux aux trois plans réflecteurs.
Les vecteurs unitaires sur les rayons sont après une, deux ou trois réflexions :
u1 = u − 2(u.n1).n1 ; u2 = u1 − 2(u1.n2).n2 ; u3 = u2 − 2(u2.n3).n3 ;
Comme les miroirs sont orthogonaux deux à, deux, on tire : u1.n2 = u.n2 et u2.n3 = u.n3
Donc u3 = u − 2[(u.n1).n1 + (u.n2).n2 + (u.n3).n3]
Et comme u = (u.n1).n1 + (u.n2).n2 + (u.n3).n3, on tire u3 = −u.
Applications :
Cette propriété est utilisée dans les catadioptres des véhicules. Ils sont constitués par un ensemble de petits coins de cube précédés de lentilles demi-boule qui augmentent la directivité.
On a déposé sur la Lune plusieurs panneaux de coins optiques. On les éclaire avec un laser à impulsion placé au foyer d'un télescope pointé sur le réflecteur et on mesure le temps entre le départ de l'impulsion et son retour sur Terre. Avec cette méthode, il est possible de mesurer la distance Terre - Lune avec une précision de quelques centimètres.
