Optique géométrique
Lentilles épaisses
Une lentille est constituée de deux dioptres dont l'un au moins est sphérique. L'épaisseur est la distance entre les sommets des dioptres mesurée sur l'axe optique. Si l'épaisseur de la lentille est négligeable devant les rayons de courbures des deux faces, la lentille est dite mince. Dans le cas contraire, c'est une lentille épaisse.
Selon les positions relatives des centres des dioptres on peut avoir six formes différentes de lentilles.
Trois sont à bords minces : la lentille biconvexe, la lentille plan-convexe et le ménisque à bords minces.
Trois sont à bords épais : la lentille biconcave, la lentille plan-concave et le ménisque à bords épais.
Sur le schéma, les
six types de lentilles sont présentées éclairées par un faisceau parallèle (objet à l'infini). L'image finale est donc le foyer image de cette lentille.
Les rayons émergents sont tracés rigoureusement en utilisant les lois de Descartes.
On peut noter que les lentilles à bords minces sont convergentes et celles à bords épais divergentes.
Deux boutons [+] et [−] permettent de faire varier l'ouverture de la lentille. On peut constater que pour les grandes ouvertures qui correspondent à des rayons émergents inclinés sur l'axe, l'image du foyer n'est plus ponctuelle : il n'y a plus stigmatisme.
Éléments cardinaux d'une lentille épaisse
Le dioptre sphérique : un système centré
 |
L'intersection entre un rayon parallèle à l'axe et le rayon émergent étant le dioptre, les points principaux sont confondus avec S. |
Les distances focales sont f = SF = n.SC / (n − n') et f ' = SF' = n'.SC / (n' − n).
La vergence du dioptre est donc V = − n / f = n' / f ' = (n' − n) / SC
Foyers et plans principaux
La lentille est définie par les caractéristiques des deux dioptres et par son épaisseur.
Le dioptre 1 a pour foyers F1 et F'1 pour distance focale f1 et f '1 et pour sommet S1.
Le dioptre 2 a pour foyers F2 et F'2 pour distance focale f2 et f '2 et pour sommet S2.
Comme pour les systèmes centrés, on caractérise l'épaisseur e = S1S2 à partir de Δ = F'1F2
En effet, on a Δ = F'1S1 + S1S2 + S2F2 = − f '1 + e + f2
Position du foyer image
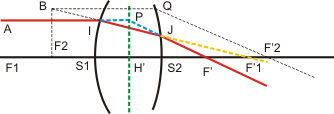 |
Un rayon incident parallèle à l'axe AI rencontre le dioptre d'entrée en I. Il se réfracte suivant IF'1 qui coupe le dioptre de sortie en J. Après réfraction sur le second dioptre, il émerge selon JF'. |
En utilisant les relations établies pour les systèmes centrés, on a F'2F' = − f2.f '2 / Δ.
On en déduit que S2F' = f '2.(Δ − f2) / Δ.
On peut aussi retrouver cette expression à partir de la figure ci-dessus.
Distances focales.
L'expression générale de la distance focale image f ' = − f '1.f '2 / Δ permet de déduire de la position de F' celle du plan principal image.
Soient R1 et R2 les valeurs algébriques des rayons de courbure des deux dioptres, n, N, n' les indices des milieux successifs et e = S1S2 l'épaisseur de la lentille.
Les vergences des dioptres sont :
V1 = (N − n) / R1 et V2 = (n' − N) / R2.
La relation de Gullstrand permet d'écrire que la vergence de la lentille est : V = V1 + V2 − V1.V2.e / N
On montre de même que la distance focale objet est donnée par f = f1.f2 / Δ
Remarque
f ' / f = − f '1.f '2 / f1.f2 = − (f '1 / f1).(f '2 / f2) = − (N / n) / (n' / N) = − n' / n
Le rapport des distances focales est l'opposé du rapport des indices des milieux extrêmes.
Lentille
épaisse placée dans l'air
Dans ce cas n = n' = 1 : les distances focales sont opposées.
A partir des expressions des vergences V1 = (N − 1) / R1 et V2 = (1 − N) / R2, on peut écrire :
f1 = − R1 / (N − 1) f '1 = R1.N / (N − 1) f2 = R2.N / (N − 1) f '2 = − R2 / (N − 1)
Δ = F'1S1 + S1S2 + S2F2 = − f '1 + e + f2 = e + (R2 − R1).N / (N − 1).
Dans ce cas l'expression de la vergence se simplifie et donne :

Si l'épaisseur est négligeable devant les valeurs des rayons de courbure des faces, on obtient :

Lentille avec une face plane
 |
Un incident issu du foyer objet émerge dans ce cas parallèle à l'axe optique : Le plan principal objet est donc confondu avec le dioptre d'entrée. H et S1 sont confondus. |
Centre optique
Le centre optique est le point de l'axe (pouvant être intérieur ou extérieur au segment S1S2) tel qu'à tout rayon incident passant par ce point correspond un rayon émergent parallèle au rayon incident.
 |
Par les centres C1 et C2 des dioptres, on mène deux parallèles qui coupent les dioptres sphériques en I et J. De même C1J est normal au dioptre de sortie. Si i' est l'angle d'émergence on pourra écrire la relation: sin i' = N . sin r Donc : i = i'. |
Examinons les triangles C1OJ et C2OI puis les triangles C1S2J et C2S1I.
Ils sont semblables deux à deux. On en déduit la série d'égalités :
OC1 /OC2 = C1I / C2J = S1C1 / S2C2 = (OC1 − S1C1) / (OC2 − S2C2) = OS1 / OS2 = R1 / R2.
On tire OS2 =S1S2. R2 / (R2 − R1)
O partage le segment S1S2 dans le rapport du rayon des faces.
Pour une lentille biconvexe ou biconcave, les rayons sont de signe contraire : O est à l'intérieur de la lentille.
Pour les ménisques, les rayons sont de même signe : O est à l'extérieur de la lentille.
Pour les lentilles avec une face plane, le rayon R2 étant infini, le rapport est nul et le centre optique est confondu avec le sommet de la face courbe.
Exemples des lentilles épaisses
Lentille boule placée dans l'air
La lentille boule est une sphère homogène d'indice N.
Son centre C est un centre de symétrie.
Tout rayon passant par C traverse les dioptres normalement
et n'est pas dévié.
Le centre optique O et les points nodaux N et N' sont confondus avec le centre de la sphère.
Comme les milieux extrêmes sont identiques, les distances focales sont opposées et les points principaux H et H' sont confondus avec les points nodaux.
Les plans principaux sont confondus avec le plan normal à l'axe passant par le centre.
Si F'1 est le foyer image du dioptre de sortie, tout rayon passant par F1 est parallèle à l'axe optique à l'intérieur de la lentille donc le point antinodal A' est confondu avec F'1.
Comme A' et N' sont symétriques par rapport à F' on a : CF' = ½.CF'1.
Pour un dioptre sphérique CF'1 = N.R / (N − 1).
La distance focale de la lentille boule est donc F' = ½.N.R / (N − 1).
On en déduit que le foyer image est distance du sommet de sortie de la quantité S2F' = ½.(2 − N).R / (N − 1).
Le foyer objet est symétrique du foyer image par rapport à C.
Sur la figure, déplacer l'objet (vert) en le glissant avec la souris.
Vérifier les formules de conjugaison sachant que N = 1,5 :
Origines aux foyers
FA.F'A' = HF.H'F'
Origines aux points principaux :
1 / H'A' − 1 / HA = − 1 / HF = 1 / H'F' = 1 / f '
Grandissement linéaire γ = A'B' / AB = − HF / FA = − F'A' / H'F'
Examiner la situation quand l'objet est à l'abscisse −3R.
Lentille demi-boule placée dans l'air
Cette lentille est une demi-sphère homogène d'indice N.
Cette lentille ayant une face plane le centre optique est confondu avec le sommet du dioptre de sortie.
On peut utiliser les formules générales mais il est ici plus simple d'utiliser le fait qu'un rayon parallèle à l'axe traverse la face plane sans déviation.
Il émerge en coupant l'axe optique en F' qui est à la fois le foyer image du dioptre de sortie et de la lentille.
Le plan principal image P' est le plan tangent à la sphère au sommet S = H'.
La distance focale est f ' = H'F' = R / (n − 1).
Pour les rayons passant par S, la lentille se comporte comme une lame à faces parallèles : Le point nodal N est le conjugué de S dans le dioptre plan d'entrée et CN = CS / n = R / n.
Comme les milieux extrêmes sont identiques les distances focales sont opposées HF = − H'F'.
On obtient la position de F à partir de la relation FN = H'F'. On a aussi NN' = HH' = R(1 − 1 / n).
