Optique géométrique

---

Lentilles minces

Une lentille est dite mince si son épaisseur est négligeable devant les rayons de courbure de ses faces.
Les sommets S1 et S2 des faces sont confondus et les plans principaux sont confondus avec le plan de la lentille car tout rayon parallèle à l'axe rencontre dans ce plan le rayon émergent correspondant :
Les points principaux H et H' sont confondus avec le sommet S.

Pour une lentille épaisse, la position du centre optique est donnée par la relation OS2 =S1S2. R2 / (R2 − R1).
On pourra considérer que O et S sont confondus si l'épaisseur S1S2 est petite devant la valeur absolue de la différence des valeurs algébriques des rayons de courbure R2 − R1.

On peut utiliser les formules générales obtenues lors de l'étude des lentilles épaisses en prenant une épaisseur nulle e = 0. En particulier, l'expression de la vergence d'une lentille mince est donnée par :

 Types de lentilles minces

Cette expression de la vergence permet de classer les lentilles minces en deux types :

Lentilles convergentes

La vergence est positive. La distance focale image OF' = f ' est positive. La distance focale objet f = − f ' est négative.
Les deux foyers sont réels : Le foyer objet est situé dans l'espace objet et le foyer image est dans l'espace image.
Les lentilles plan-convexe, biconvexe et les ménisques tels que SC1 < SC2 (ménisques à bords minces) sont convergents.

Lentilles divergentes

La vergence est négative. La distance focale image f ' est négative. La distance focale objet f est positive.
Les deux foyers sont virtuels : Le foyer objet est situé dans l'espace image et le foyer image est dans l'espace objet.
Les lentilles plan-concave, biconcave et les ménisques tels que SC1 > SC2 (ménisques à bords épais) sont divergents.

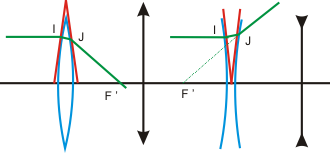Ces résultats se retrouvent simplement en considérant qu'une lentille à bords minces agit sur un rayon comme un prisme de petit angle ayant sa base confondue avec l'axe et qui rabat vers l'axe optique un rayon parallèle à l'axe. Une lentille à bords épais se comporte comme un prisme de petit angle ayant son sommet placé sur l'axe optique. Cette remarque justifie les schémas utilisés pour représenter les lentilles minces.

 Relations de conjugaison

Construction des images

Pour les constructions des images, on utilise deux des trois rayons incidents issus de B suivants :

• Le rayon qui passe par le centre optique et qui n'est pas dévié.
• Le rayon parallèle à l'axe qui émerge en passant par le foyer image.
• Le rayon qui passe par le foyer objet et qui émerge parallèle à l'axe.

L'intersection des deux rayons définit le point B' image de B. Le point A' image de A est situé sur la normale à l'axe passant par B'.

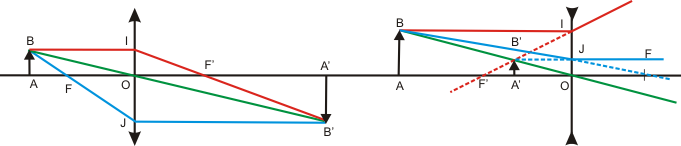
Cas particulier : B est à l'infini
Dans ce cas B' est dans le plan focal image et il suffit de tracer le rayon BO pour obtenir B'.

Relations de conjugaison

On peut utiliser les relations générales établies pour les lentilles épaisses en faisant e = 0. Il est possible d'établir directement ces relations en utilisant les figures ci-dessus.

Les triangles ABO et A'B'O sont semblables : A'B' / AB = γ = OA' / OA

Les triangles ABF et OJF sont semblables : γ = OJ / AB = FO / FA .
De même les triangles OIF' et A'B'F' sont semblables : γ = A'B' / OI = F'A' / F'O .

On déduit la relation de Newton F'A'.FA = OF.OF' = − f '².

On peut écrire cette relation sous le forme (F'O + OA').(FO + OA) = − f '².
F'O.FO + OA'.FO + F'O.OA + OA'.OA = − f '².
OA'.FO + F'O.OA = − OA'.OA
En divisant les deux membres par −OF'. OA'.OA, on tire :

Exemples de construction

Ce programme donne quelques exemples de construction des images données par une lentille mince.

 Analyse des formules de conjugaison.

La relation de conjugaison donne : OA' = OA.f ' / (OA + f ') C'est l'équation d'une hyperbole équilatère dont les asymptotes sont OA = −f' et OA' = f '. Le graphique ci-contre représente la variation de la position de l'image (OA') en fonction de la position de l'objet (OA). Objet et image sont homothétiques par rapport au centre optique. Donc l'image est droite si elle est du même côté de la lentille que l'objet c'est-à-dire si objet et image sont de nature différente. L'image est inversée si elle est de l'autre côté de la lentille que l'image c'est-à-dire si objet et image sont même nature. Les deux sont réels ou virtuels. Lentille convergente (f ' > 0) Objet situé à − ∞ L'image réelle est dans le plan focal image.

Objet entre − ∞ et 2f : L'image est réelle, inversée et plus petite que l'objet.
Objet situé à 2f : L'image est réelle, inversée et égale à l'objet. Cette position correspond aux plans antiprincipaux.
Objet entre 2f et f : L'image est réelle, inversée et plus grande que l'objet.
Objet dans le plan focal objet : L'image est à l'infini.
Objet entre F et O : L'image est virtuelle, droite et plus grande que l'objet.
Objet entre O et +∞ : L'image est virtuelle, droite et plus petite que l'objet.

Lentille divergente (f '< 0)

Objet situé à − ∞ : L'image virtuelle est dans le plan focal image.
Objet entre − ∞ et O : L'image est virtuelle, droite et plus petite que l'objet.
Objet entre O et F' : L'image est réelle, droite et plus grande que l'objet.
Objet entre F' et 2f ' : L'image est virtuelle, renversée et plus grande que l'objet.
Objet à 2 f ' : L'image est virtuelle, renversée et égale l'objet. Cette position correspond aux plans antiprincipaux..
Objet entre 2f ' et +∞ : L'image est virtuelle, renversée et plus petite que l'objet.

Bien noter que sur la figure, les rayons réels sont tracés en trait plein et le faisceau issu du point source (ou qui converge vers ce point dans le cas des objets virtuels) est représenté en rose.

 Associations de lentilles minces.

Lentilles minces accolées

Les centres optiques des lentillesL1 et L2 de vergences V1 et V2 sont confondus. D'après la relation de Gullstrand, l'ensemble est identique à une lentille unique dont la vergence est V = V1 + V2.

On peut retrouver directement cette relation à partir des relations de conjugaison.
On désigne par A l'objet, A1 l'image de A dans L1 (qui sert d'objet pour L2) et A' l'image finale.
On a : 1 / OA1 − 1 / OA = 1 / f '1 ainsi que 1 / OA' − 1 / OA1 = 1 / f '2
En faisant la somme des deux relations, on tire : 1 / OA' − 1 / OA = 1 / f '1 +1 / f '2 = D1 + D2.

Remarques
Il peut paraître absurde d'accoler deux lentilles alors que l'on peut faire la même chose avec une lentille unique. En fait on accole souvent deux lentilles de nature différente et faites avec des verres différents pour obtenir une lentille achromatique.
Si V1 = − V2 l'association des deux lentilles est équivalente à une lame à faces parallèles. Si la vergence d'une lentille est connue, on en déduit celle de l'autre. Avant l'apparition des frontofocomètres cette méthode dite de neutralisation était utilisée par les lunetiers pour déterminer la distance focale des verres de lunettes.

Doublet de lentilles minces

Un doublet est constitué par l'association de deux lentilles L1 et L2 de focales f '1 et f '2 dont les centres optiques sont séparés par la distance e = S1S2.
Un doublet est défini par son symbole, ensemble des nombres algébriques m, n et p, souvent entiers et tels que :
f '1 / m = e / n = f '2 / p = a.
Tous les doublets ayant même symbole sont homothétiques.
Beaucoup de systèmes centrés (microscope, lunettes, viseurs...) peuvent être schématisés par un doublet constitué d'un objectif et d'un oculaire.

Position du foyer image F'

F' est le conjugué de F'1 par rapport à la lentille L2.

On pose F2F'1 = Δ = f '1 + f '2 − e.

Comme S2F'1 = f '1 − e, on a : 1 / S2F' = 1 / (f '1 − e) + 1 / f '2

Donc : S2F' = f '2. (f '1 − e) / (f '1 + f '2 − e) = f '2. (f '1 − e) / Δ

Vergence et distances focales

D'après la relation de Gullstrand, on a : V = 1 / f '1 + 1 / f '2 − e / f' 1.f '2 = Δ / f '1.f '2.

Les distances focales sont donc : f ' = − f = f '1.f '2 / Δ

Comme la distance focale et la position de F' sont connues, il est possible de déterminer la position de tous les éléments principaux du doublet.

On peut aussi noter que F' étant le conjugué de F'1 par rapport à la lentille L2 les relations de Newton donnent :
F2F'1.F'2F' = − f '²2 soit F'2F' = − f '²2 / Δ.
On a de même F1F = − f '²1 / Δ.

Doublet symétrique
Si les deux lentilles sont identiques le doublet est symétrique. Les distances focales sont identiques. Le centre optique est le milieu de S1S2 et les éléments cardinaux sont tous symétriques par rapport à O.

Doublet afocal

Si le foyer image de la première lentille coïncide avec le foyer objet de la seconde alors Δ = 0 et e = f '1 + f '2. Les foyers sont à l'infini et le doublet est dit afocal : L'image d'un objet situé à l'infini est à l'infini. Si l'objet se déplace, l'image conserve une dimension constante γ = A'B' / AB = − f '2 / f '1.

Il est possible de constituer un système afocal de grandissement donné en associant deux lentilles minces dont les distances focales sont dans le rapport choisi. C'est le cas de la lunette astronomique.

Utilisation du programme

La valeur du paramètre a est calculée pour que l'on puisse déplacer l'objet d'une valeur 2f1 devant L1 et que l'on puisse également observer une distance 2f '2 derrière L2.
Choisir les valeurs de m, n et p avec les curseurs. 0< m <= 10; 0 ≦ n <= 10 et −11< p < 11 (0 exclu).
Les rayons sont tracés en utilisant les relations de conjugaison. Quand l'objet passe sur un foyer, le tracé des rayons devient incohérent.
L'objet Ob (en jaune) peut être déplacé avec la souris. L'image I1 de Ob donnée par L1 est tracée en rouge. L'image I2 (image finale) de I1 donnée par L2 est tracée en vert.
Les petites graduations sur l'axe optique sont espacées de 20 divisions, les grandes de 100 divisions. Les divisions ont une valeur arbitraire car deux doublets de même formule sont homothétiques.
Les deux traits gris horizontaux permettent (dans certains cas) de trouver la position des plans principaux et anti-principaux (plans de gain +1 et −1).
Dans un cadre sont affichées les caractéristiques du doublet ainsi que celle du système équivalent.

Exercices

• Vérifier les formules de conjugaison pour des valeurs arbitraires de m, n et p.
• Étudier en détail les doublets de formule 3, 2 et 1 (oculaire de Huygens) et 3, 2 et 3 (oculaire de Ramsden). Ce dernier doublet est symétrique.
• Constituer et étudier un système afocal.