Associations de lentilles minces

 Lentilles minces accolées.

Les centres optiques des lentilles L₁ et L₂ de vergences V₁ et V₂ sont confondus. D'après la relation de Gullstrand, l'ensemble est identique à une lentille unique dont la vergence est V = V₁ + V₂.

On peut retrouver directement cette relation à partir des relations de conjugaison.
On désigne par A l'objet, A₁ l'image de A dans L₁ (qui sert d'objet pour L₂) et A' l'image finale.
On a : 1 / OA₁ − 1 / OA = 1/ f '₁ ainsi que 1/ OA' − 1/ OA₁ = 1 / f '₂
En faisant la somme des deux relations, on tire : 1 / OA' − 1 / OA = 1/ f '₁ + 1 / f '₂ = V₁ + V₂.

Remarques

1. Il peut paraître absurde d'accoler deux lentilles alors que l'on peut faire la même chose avec une lentille unique. En fait on accole souvent deux lentilles de natures différentes et fabriquées avec des verres différents pour obtenir une lentille achromatique.
2. Si V₁ = − V₂ l'association des deux lentilles est équivalente à une lame à faces parallèles. Si la vergence d'une lentille est connue, on en déduit celle de l'autre. Avant l'apparition des frontofocomètres cette méthode dite de neutralisation était utilisée par les lunetiers pour déterminer la distance focale des verres de lunettes.
3. Dans l'application faire e = 0 pour étudier ce cas.
   
   
   

 Doublet de lentilles minces.

Un doublet est constitué par l'association de deux lentilles L₁ et L₂ de focales f '₁ et f '₂ dont les centres optiques sont séparés par la distance e = S₁S₂.
Un doublet est défini par son symbole, ensemble des nombres algébriques m, n et p, souvent entiers et tels que :
f '₁ / m = e / n = f '₂ / p = a.
Tous les doublets ayant même symbole sont homothétiques.
Beaucoup de systèmes centrés (microscope, lunettes, viseurs...) peuvent être schématisés par un doublet constitué d'un objectif et d'un oculaire.

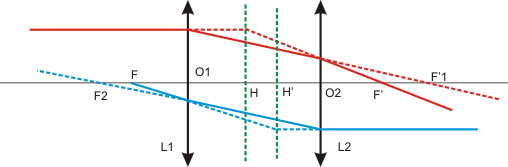
Position du foyer image F'

F' est le conjugué de F'₁ par rapport à la lentille L₂.

On pose F₂F'₁ = Δ = f '₁ + f '₂ − e.

Comme S₂F'₁ = f '₁ − e, on a : 1/ S₂F' = 1/ (f '₁ − e) + ₁ / f '₂

Donc : S₂F' = f '₂. (f '₁ − e) / (f '₁ + f '₂ − e) = f '₂. (f '₁ − e) / Δ

Vergence et distances focales

D'après la relation de Gullstrand, on a : V = 1 / f '₁ + 1 / f '₂ − e / f' ₁.f '₂ = Δ / f '₁.f '₂.

Les distances focales sont donc : f ' = − f = f '₁.f '₂ / Δ

Comme la distance focale et la position de F' sont connues, il est possible de déterminer la position de tous les éléments principaux du doublet.

On peut aussi noter que F' étant le conjugué de F'₁ par rapport à la lentille L₂ les relations de Newton donnent :

F₂F'₁.F'₂F' = − f '²₂ soit F'₂F' = − f '²₂ / Δ.

On a de même F₁F = − f '²₁ / Δ.

Doublet symétrique
Si les deux lentilles sont identiques le doublet est symétrique. Les distances focales sont identiques. Le centre optique est le milieu de S1S2 et les éléments cardinaux sont tous symétriques par rapport à O.

 Doublet afocal

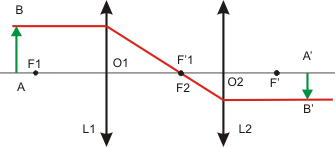Si le foyer image de la première lentille coïncide avec le foyer objet de la seconde alors Δ = 0 et e = f '1 + f '2. Les foyers sont à l'infini et le doublet est dit afocal : L'image d'un objet situé à l'infini est à l'infini. Si l'objet se déplace, l'image conserve dans ce cas une dimension constante γ = A'B' / AB = − f '2 / f '1.

Il est possible de constituer un système afocal de grandissement donné en associant deux lentilles minces dont les distances focales sont dans le rapport choisi. C'est le cas de la lunette astronomique.

 Visualisation des cas possibles.

Utilisation du programme

Trois curseurs permettent de choisir les valeurs de f '₁, e et f '₂. Les valeurs des focales comprises entre −10 et +10 sont volontairement exclues.
Deux cases à cocher permettent de placer l'objet à l'infini et de tracer ou non les foyers et les plans principaux.
Les rayons sont tracés en utilisant les relations de conjugaison.
L'objet Ob (en jaune) peut être déplacé avec la souris. L'image I₁ de Ob donnée par L₁ est tracée en magenta. L'image I₂ (image finale) de I₁ donnée par L₂ est tracée en rouge.
Si l'objet est à l'infini, en glissant le point jaune, on modifie l'inclinaison du faisceau.
Les petites graduations sur l'axe optique sont espacées de 20 divisions, les grandes de 100 divisions. Les divisions ont une valeur arbitraire car deux doublets de même formule sont homothétiques.
Les deux traits horizontaux tracé en bleu foncé permettent (dans certains cas) de trouver la position des plans principaux et anti-principaux (plans de gain + 1et − 1).
Le rayon central du faisceau incident est tracé volontairement horizontal. L'examen du rayon émergent correspondant facilite l'étude des systèmes afocaux.

Dans le cadre on affiche les positions de l'objet, celles des images ainsi que les caractéristiques du système équivalent.

Exercices

• Vérifier les formules de conjugaison pour des valeurs arbitraires de m, n et p.
• Étudier en détail les doublets de formule 3, 2 et 1 (oculaire de Huygens) et 3, 2 et 3 (oculaire de s). Ce dernier doublet est symétrique.
• Constituer et étudier un système afocal.