Instruments d'optique

---

 

 Classification des instruments

Il est habituel de classer les instruments en deux grandes catégories : ceux qui donnent une image virtuelle ou subjective et ceux qui donnent une image réelle ou objective.

Instruments subjectifs

Ce type d'instrument donne en général une image virtuelle souvent agrandie d'un objet très petit ou qui semble très petit car situé à grande distance de l'observateur.
Dans cette catégorie, on peut classer loupes, microscopes, viseurs, lunettes et télescopes. Ces instruments (sauf la loupe) comportent un objectif et un oculaire.
L'objectif, convergent, donne de l'objet une image réelle qui est observée à travers un oculaire. Celui-ci donne une image virtuelle agrandie de l'image objective.

Instruments objectifs

Ces instruments donnent une image réelle d'un objet réel formée par un objectif.
On trouve dans cette catégorie les projecteurs, les objectifs photographiques et l'œil.

Caractéristiques d'un instrument

Les instruments sont caractérisés par diverses caractéristiques qui influent sur le choix de l'utilisateur.

• Grandeur de l'image obtenue : selon les cas on la caractérise par le grandissement, le grossissement ou la puissance.
• Le pouvoir séparateur qui correspond à la finesse des détails observables.
• Le champ qui correspond à la portion de l'objet observable.
• La clarté qui correspond au rapport entre les intensités lumineuses obtenues avec l'instrument et sans lui.

 Grandissement, Grossissement et Puissance.

Grandissement linéaire

C'est le rapport entre une dimension de l'objet et de la même dimension de l'image. Cette notion ne présente un intérêt que pour des images réelles d'objets situés à distance finie.

Puissance

Cette notion concerne les loupes et microscopes.
La puissance est définie comme le rapport entre l'angle θ' sous lequel on voit l'objet à travers l'instrument et la grandeur effective y de l'objet : P = θ' / y
L'angle étant exprimé en radian et la distance en mètre, P à la dimension de l'inverse d'une longueur et s'exprime donc en dioptrie.

Puissance intrinsèque.
Dans le cas ou l'objet est placé au foyer objet d'un instrument de distance focale f, l'image est à l'infini et l'angle sous lequel elle est vue du foyer image est θ' = y / f.
La puissance de l'instrument utilisé dans ces conditions est la puissance intrinsèque Pi = 1 / f.

Grossissement

Objets proches (loupes et microscopes).
Le grossissement est le rapport de l'angle θ' sous lequel on voit une dimension de l'objet à travers l'instrument et de l'angle maximum θ sous lequel on la voit à l'œil nu. G = θ' / θ
Si δ est la distance minimum de vision distincte θ≈ y / δ. Soit G = θ' / y .δ = P.δ
Le grossissement dépend de l'instrument et de l'observateur.
On définit donc un grossissement commercial qui correspond à une valeur de δ égale à 25 cm : Gi = Pi / 4

Objets distants (lunettes et télescopes).
Le grossissement est le rapport de l'angle θ' sous lequel on voit une dimension de l'objet à travers l'instrument et de l'angle θ sous lequel on la voit à l'œil nu. G = θ' / θ
Pour caractériser l'instrument, on suppose que la mise au point est faite sur l'infini et le grossissement est alors intrinsèque.

 Pouvoir séparateur.

Diffraction

Pour un appareil parfaitement stigmatique et selon l'optique géométrique l'image d'un point est un point. En réalité à cause le la diffraction de la lumière l'image d'un point est une tache dont la forme est fonction de la pupille. Pour une pupille circulaire la tache est la tache d'Airy. Le rayon du premier anneau noir est donné par la relation r = 1,22 λ / 2 n.sin α (α étant l'angle maximum d'inclinaison des rayons de la pupille). On admet que deux points lumineux sont séparés si leur distance est égale au rayon du premier anneau noir.
Pour visualiser le phénomène voir cette page.

Récepteur

Les détecteurs (œil, film, CCD) d'images ont une structure granuleuse. Deux points ne peuvent être séparés que si leurs images se forment sur deux grains détecteurs différents. Pour l'œil l'expérience montre que la limite de résolution dépend principalement du diamètre effectif de la pupille d'entrée de l'œil et que la valeur optimum du diamètre est 0,5 mm.
L'usage d'un instrument est optimal quand le pouvoir séparateur n'est limité que par la diffraction.

 Champ et clarté

Champ

Le champ est la région de l'espace visible à travers l'instrument. Les faisceaux lumineux issus de l'objet observé arrivent à l'œil après traversé de l'instrument. Ils rencontrent des diaphragmes qui limitent les faisceaux transmis. Ces diaphragmes sont constitués par les montures des lentilles et par des écrans dont le rôle est d'éliminer des rayons inutiles ou trop inclinés sur l'axe.

Clarté

La clarté est le rapport entre les éclairements de la rétine a travers l'instrument et à l'œil nu. Elle dépend entre autres du facteur de transmission de l'instrument.
Les pertes résultent :
* Des réflexions sur la surface des verres (4 % en incidence normale pour un verre non traité. Ces réflexions produisent aussi des rayons parasites qui peuvent dégrader l'image.
* De l'absorption par le verre : Pour les verres récents elle est dans le visible de l'ordre de 1 / 1000 par centimètre

 Loupe

A l'œil nu l'observateur voit l'objet placé à son ponctum proximum δ sous l'angle θ = AB / δ. A travers la loupe il le voit sous l'angle θ' = A'OB' (O est le centre optique de l'œil). En général c'est la pupille de l'œil qui limite l'ouverture des faisceaux utiles.

Mise au point et profondeur de champ

Un déplacement l'objet provoque le déplacement de l'image.
O étant le centre optique de l'œil, on pose D = A'O : c'est la distance de visée.
On pose d = F'O qui est la position de l'œil par rapport à la loupe.
La formule de Newton donne FA.F'A' = − f ².
Comme F'A' = F'O + OA' = d − D alors FA = f ² / (D − d).(a)
Cette relation permet de déterminer comment il faut placer la loupe pour observer l'image à une distance donnée.

Profondeur de champ
Soient A₁ et A₂ les positions de l'objet qui correspondent à des positions de l'image qui sont le ponctum remotum Δ et le ponctum proximum δ de l'observateur.
De la relation (a), on tire A₁A₂ = FA₂ − FA₁ = f². (Δ − δ) / (Δ − d). (δ − d).
Pour un œil normal (emmétrope), le ponctum remotum est situé à l'infini : A₁A₂ = FA₂ = f ² / (δ − d) ≈ f ² / δ

Grossissement et puissance

Par définition le grossissement est G = θ' / θ.
G = (A'B' / D) / (AB / δ) = δ.A'B' / D.AB = − δ.F'A' / D.f = δ.(1 − d / D) / f
G dépend de la loupe (f), de la position de l'œil et de la loupe (d et D) et de la distance minimum de vision (δ).
Si on place la pupille de l'œil au niveau du foyer image (d = 0) alors le grossissement est dit intrinsèque Gi = δ / f.
Comme le grossissement intrinsèque varie avec l'utilisateur, on définit le le grossissement commercial en prenant δ = 0, 25 m.
Si D est la vergence en dioptries de la loupe alors Gc = D / 4.

Par définition la puissance est P = θ' / AB.
P = G. θ / AB = G / δ soit P = (1 − d / D) / f .
Si on place la pupille de l'œil au niveau du foyer image (d = 0) alors P = 1 / f.

Une loupe de bonne qualité comporte plusieurs lentilles pour obtenir une bonne correction des aberrations chromatiques et géométriques. Le grossissement maximum d'une loupe bien corrigée est de l'ordre de 15.

 Oculaires

Un oculaire permet d'observer en l'agrandissant l'image réelle donnée par un objectif. C'est une loupe améliorée que l'on rencontre dans de nombreux instruments : microscopes, lunettes terrestres et astronomique, télescopes, viseurs...

Il existe deux types d'oculaires :
Oculaire divergent : C'est un système divergent placé avant le foyer image de l'objectif. Si celui-ci fournit une image inversée, elle est vue droite avec un oculaire divergent. C'est l'oculaire de la lunette de Galilée.

Oculaire convergent : C'est l'équivalent d'une loupe placée après le foyer image de l'objectif. Si l'objectif donne une image inversée, celle-ci est vue inversée avec ce type d'oculaire. Avec des jumelles, il faut ajouter un redresseur d'image pour utiliser cette configuration.

L’utilisation d’oculaires constitués de plusieurs lentilles permet d’augmenter le champ global (pour un doublet, la distance entre le foyer objet et la lentille d’entrée est en général inférieure à la distance focale d’une lentille unique de même focale.)
Les oculaires comportent de une lentille (oculaire de Galilée) à une dizaine de lentilles.

Oculaire d'Huygens 

Système optique équivalent (Approximation de Gauss) L'oculaire d'Huygens est un doublet formé de deux lentilles convergentes de distances focales f1= 3a, f2 = a, dont les sommets S1 et S2 sont distants de 2a. (formule 3 – 2 – 1). Les foyers images des deux lentilles F’1 et F’2 sont donc confondus. La vergence du système est donnée par la formule de Gullstrand : V = V1 + V2 − e.V1.V2 On pose D = F'1F2 = −f '1 + e − f '2 (intervalle optique).

La distance focale image est f ' = − f '₁.f '₂ / D
F'2F' = − f₂.f '₂ / D (Le foyer image du système est le conjugué de F'₁ dans L2);
 F₁F = f₁.f '₁ / D (Le foyer objet du système est le conjugué de F₂ dans L1);
La distance focale est égale à 3a / 2.
La figure indique une méthode graphique de détermination des éléments principaux du système équivalent à ce système épais. Les foyers objet (F) et image (F’) sont à la distance a /2 de S₂.
Le plan principal image (H’) est situé au milieu des deux lentilles et le plan principal objet est confondu avec le plan focal image des deux lentilles. (Les plans principaux sont les plans de grandissement +1).
Le foyer image est réel : l'oculaire est convergent
Le foyer objet se trouve en arrière de S1 : l'oculaire est dit négatif (FoS₁ < 0).

En utilisation normale, cet oculaire permet (en plaçant l’œil en H) d’observer une image formée dans son plan focal objet par un objectif. La première lentille donne de cette image (qui est virtuelle) une image réelle située dans le plan focal de la seconde lentille. L’image finale est donc à l’infini ; elle est observée sous un angle a.
Le diaphragme tracé en bleu correspond à la pupille de l'œil.
Le système se comporte comme une loupe. Il ne permet pas l’utilisation d’un réticule puisque l'on observe un objet virtuel. Comme l’angle d’observation final est indépendant de la couleur de la lumière incidente, cet oculaire n’a pas d’achromatisme apparent.

Achromatisme apparent :
On suppose qu'un objectif corrigé de l'aberration chromatique est suivi par un oculaire.
Pour avoir achromatisme en utilisation normale (image à l'infini) , il faut que les dimensions des images colorées soient toutes identiques. Ceci suppose qu'elles sont vues sous le même angle. La distance focale du doublet Φ doit être indépendante de la longueur d'onde. Or pour un doublet, on a : 1 / Φ = 1 / φ₁ +   1 / φ₂ − e / φ₁. φ₂. (a)
Il y a achromatisme si d(1 / Φ) = 0 soit dφ₁ / φ₁² + dφ₂ / φ₂² − e.(dφ₁ / φ₁+ dφ₂ / φ^₂) / φ₁. φ₂ = 0. (b)
Si les lentilles de l'oculaire sont faites d'un même verre on a : dφ₁ / φ₁= dφ₂ / φ^₂ = A.
La relation (2) devient : A / φ₁ +   A / φ₂ − 2.A.e / φ₁. φ₂ = 0 soit φ₁ +   φ₂ = 2.e
Cette relation est vérifiée pour les oculaires d'Huygens de formules 3-2-1 ou 4-3-2.

 Microscopes

Un microscope est l'association :
D'un objectif convergent de distance focale faible f ’₁ qui donne d'un objet AB situé en avant de son foyer objet une image réelle A'B' et qui est γ₁ fois plus grande. γ₁ = A'B' / AB est le grandissement de l'objectif.
et d'un oculaire convergent de distance focale f ’₂ qui permet d'observer cette image intermédiaire en la grossissant.
Pour éviter la fatigue oculaire, il est souhaitable que l'image finale A"B" soit à l'infini et donc que A'B' se forme dans le plan focal de l'oculaire. Pour obtenir une mise au point facile, on laisse constante la distance objectif-oculaire et on déplace l'ensemble.

Soit Δ = F'₁F₂ l'intervalle optique du microscope. Par convention on prend souvent Δ =150 mm.
Le grandissement propre de l'objectif est donc γ₁ = Δ / f₁.

L'oculaire est du type Huyghens (doublet négatif). Sa distance focale varie entre 12 mm et 45 mm.
L'objectif travaille à grande ouverture et la condition d'aplanétisme est réalisée pour les points A et A' : n sin u. AB = A'B'. sin u'
Les lentilles constituant l'objectif réduisent progressivement l'ouverture des faisceaux et on peut considérer que le faisceau utile est paraxial, on peut écrire : n sin u. AB = A'B'.u '
γ₁ = n. sin u / u' = On / u '.
On est appelé "ouverture numérique" de l'objectif.

 Elements cardinaux

D'après la relation de Gullstrand la distance focale image est f ' = − f '₁. f₂ / Δ. Elle est négative et très faible.
Le foyer objet F du microscope est le point de l'axe dont l'image est située à l'infini. Son image dans l'objectif est donc F₂.
La formule de Newton appliquée à l'objectif donne : F₁F . F'₁F₂ = f₁.f '₁ .
Donc F₁F = − f₁² / Δ.
Avec Δ = 15 cm et f₁ = 5 mm, on a = F₁F = − 0,6 mm.
Le foyer objet F du microscope est un tout petit peu en avant du foyer objet de l'objectif.

Le foyer image F' du microscope est le point de l'axe conjugué de F'₁ par rapport à l'oculaire.
La formule de Newton appliquée à l'oculaire donne : F₂F'₁ . F'₂F' = f₂.f '₂ .
Donc F₂F' = − f₂² / Δ.
Avec Δ = 15 cm et f₂ = 3 mm, on a = F₁F = − 6 mm.
Le foyer image F' du microscope est un tout petit peu en arrière du foyer image de l'oculaire.

 Cercle oculaire

Les lentilles de l'objectif ont des diamètres très faibles par rapport à la longueur du microscope : le diaphragme d'ouverture est souvent défini par le diamètre de la première lentille de l'objectif et sa distance au foyer de l'oculaire est peu différente de Δ.
Le cercle oculaire est l'image de ce diaphragme à travers le reste du système optique.
Soit P la position du diaphragme d'ouverture et P' son image..
La formule de Newton appliquée à l'oculaire donne : F₂P . F'₂P' = f₂.f '₂ . Soit F₂P' ≈− f₂² / Δ.
Le cercle oculaire est voisin du foyer image de l'oculaire. La formule précédente s'applique aussi pour les diamètres des pupilles.
Le diamètre de la pupille de sortie est beaucoup plus petit que celui de la pupille d'entrée (de l'ordre de 2 à 4 mm) : il est bien plus petit que la pupille de l'œil.

 Puissance et grossissement

La puissance est le rapport du diamètre θ ' de l'image à la longueur AB de l'objet. P = θ ' / AB.
P = θ ' / AB = (θ ' / A ' B ').( A ' B ' / AB) = P₂.γ₁
La puissance du microscope est mesurée par le produit du grandissement de l'objectif par la puissance de l'oculaire.
Le grandissement propre de l'oculaire est en fait le grossissement commercial pour une distance minimale de vision égale à 25 cm.
Si P est la puissance de l'oculaire alors G = P.d = P / 4 .
Pour la puissance intrinsèque, on a Gi = Pi / 4 = 1 / 4.f₂.
Ainsi un grossissement de 15 correspond à une distance focale de 17 mm.

Le grossissement du microscope est égal au rapport du diamètre apparent de l'image et du diamètre apparent de l'objet vu à l'œil nu à la distance minimum de vision distincte δ. Donc G = P.δ. Il varie avec l'observateur.
On prend souvent par convention δ = 25 cm et alors G = P / 4 : c'est le grossissement commercial.
Le grossissement est égal au produit du grossissement de l’objectif par la puissance de oculaire.
Un objectif de distance focale image f '₁ = 15 mm avec Δ =150 mm a un grandissement 10.
Un oculaire de distance focale image f '₂ = 25 mm a un grossissement commercial g = 1 / (4 x 0,025) = 10.
Le microscope obtenu aura un grossissement 10 x 10 = 100.

 Mise au point

L’objet doit être placé juste avant le foyer objet de l’objectif et l’image intermédiaire doit se former dans le plan focal de l’oculaire pour avoir une image finale à l'infini.
On déplace l'ensemble Objectif - Oculaire pour que l'observateur voit une image nette. Il faut que l'image finale se forme entre son ponctum proximum et son ponctum remotum. Il est préférable de faire la mise au point sur le ponctum remotum afin de ne pas avoir à accommoder. Un emmétrope forme une image à l'infini. Un myope doit rapprocher de la préparation un microscope réglé sur l'infini. Inversement un hypermétrope doit l'éloigner.

Si A est l'image d'un point de l'axe dans l'instrument du ponctum proximum et F le foyer objet du microscope, la profondeur de champ est FA. Si d est la position du centre optique de l'œil par rapport au foyer image alors FA . (d − δ) = f.f '.
Le centre optique de l'œil est très proche de F ' et FA. δ = f.f '.
Avec f = 1 mm et δ = 20 cm FA = 5 µm
La profondeur de champ d'un microscope est très petite.

 Éclairage

La préparation doit être éclairée soit par transmission ou par réflexion.
L'éclairage par réflexion est utilisé avec les loupes binoculaires qui sont en fait constituées de deux microscopes de faible grossissement jumelé. La profondeur de champ est assez grande et la vision stéréoscopique permet une vision 3D.

L'éclairage par transmission est utilisé pour les objets très minces et transparents Pour les faibles grossissements on utilise un miroir concave pour concentrer la lumière sur la plan de la préparation.
Pour les forts grossissements, on utilise un condenseur dont le rôle est de donner une image de la source dans le plan de la préparation avec une ouverture au moins égale à celle de l'objectif.

 Construction du microscope

Objectifs :
Les contraintes sont nombreuses : grande ouverture, aplanétisme, achromatisme, aberrations de sphéricité minimes. Plus l'ouverture est grande plus la construction est difficile. On arrive à de très bons résultats en multipliant le nombre de lentilles avec comme inconvénient une perte de luminosité.
Oculaires :
On utilise en principe un oculaire négatif de type Huyghens qui est achromatique. Si on veut utiliser un réticule ou un micromètre, on utilise un oculaire positif de type Ramsden.
Mécanique :
Un bon microscope comporte un pied statif stable, une potence qui supporte le corps du microscope. La partie basse du tube comporte une monture à revolver ou se vissent les objectifs. La partie supérieure reçoit les oculaires. A la base de la potence on trouve une platine porte objet qui supporte aussi le condenseur ou un miroir d'éclairage.
La mise au point est réalisée avec une crémaillère.

 Lunettes

Lunette astronomique

C’est un système optique utilisé pour augmenter le diamètre apparent des objets situés à l’infini et pour augmenter la clarté des objets sans diamètre apparent comme les étoiles.
La lunette comporte un objectif convergent de grande distance focale F et corrigé des aberrations chromatiques (doublet convergent formé par une lentille convergente et une lentille divergente de dispersions différentes) et un oculaire convergent de courte distance focale f.

L’objet étant situé à l’infini, l’image donnée par l’objectif se forme dans son plan focal image. Si la position de l’oculaire est telle que son foyer objet est confondu avec le foyer image de l’objectif, l’image finale est située à l’infini.
Dans ces conditions,la lunette astronomique est un système est afocal.
Le grossissement de la lunette est le rapport des diamètres apparents de l'image et de l'objet : G = α' / α.
Soit p₂ la puissance de l'oculaire p₂= α' / A'B'. D'autre part α = A'B' / F' et G = F '. p₂.
Si la lunette est afocale alors p₂ = 1 / f '
Le grossissement de la lunette est donc égal au rapport des distances focales G = F ' / f ’.
Le diamètre du cercle oculaire D' est alors égal à D. f ' / F '.

L'élément principal de la lunette est son objectif. De son diamètre D ' dépendent le pouvoir séparateur et la clarté.
En général l'objectif est formé de deux lentilles, l'une en crown, l'autre en flint et la détermination des quatre rayons de courbure permet de fixer la distance focale, de réaliser l'achromatismel, de corriger l'aberration longitudinale et de réaliser la condition d'aplanétisme.

L’image étant inversée, cette lunette est difficilement utilisable pour l’observation terrestre. On peut utiliser un système de miroirs (en fait un train de prismes) ou une lentille intermédiaire pour redresser l'image : on obtient alors une lunette terrestre.

Longue-vue

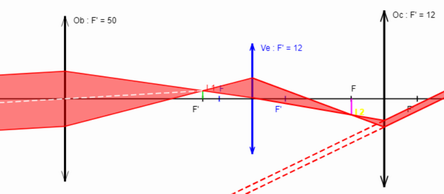Dans la longue-vue, on utilise un oculaire convergent et le redressement de l'image est obtenu en utilisant un système optique le véhicule que l'on peut schématiser par une lentille convergente (en bleu).
L'objectif donne de l'objet AB une image A₁B₁ inversée située près de son foyer image. Le véhicule donne de cette image réelle une image réelle A₂B₂ de même sens que AB. L'oculaire permet d'observer cette image. Si le foyer objet F de l'oculaire est placé en A₂B₂, l'image finale est à l'infini.
Le véhicule redresseur induit un allongement important de la lunette (de l'ordre de 4 fois la distance focale du véhicule) mais agrandit l'image donnée par l'objectif.
La longue-vue est surtout utilisée dans les viseurs de tir. L'objectif est un achromat à deux ou trois lentilles, le véhicule est constitué par un doublet de lentilles achromatiques.

Lunette à prismes

L'objectif donne d'un objet ABC une image inversée A'B'C'. Le redressement de cette image est assurée par deux prismes rectangles isocèles dont les arêtes sont orthogonales (système de Porro). Il y a réflexion totale sur les deux faces du dièdre. Chaque prisme est équivalent (si l'on omet les réfractions sur la face hypoténuse) à un ensemble de deux miroirs perpendiculaires.
Le premier prisme (arête verticale) donne de A'B'C' une image A₁B₁C₁ symétrique par rapport à un plan vertical. On a inversé la droite et la gauche. Le second (arête horizontale) donne une image A₂B₂C₂ symétrique de A₁B₁C₁ par rapport à un plan horizontal. On inverse ainsi haut et bas.
Après traversée des deux prismes l'image finale est une image totalement inversée de A'B'C'.
Les rayons étant repliés dans la lunette la longueur de celle-ci est bien plus faible que pour une longue-vue. Les trajets dans le verre des prismes augmente encore le chemin optique.

En associant deux lunettes à prismes on constitue des jumelles. Comme il faut faire coïncider les axes optiques de chaque lunette avec le centre de rotation des yeux les jumelles sont à écartement variable.
La mise au point est effectuée avec un bouton moleté qui déplace les deux oculaires par rapport aux objectifs. L'un des oculaires est aussi mobile afin de corriger la mise au point pour des yeux affectés de défauts différents.
Dans les modèles élaborés des œilletons permettent d'effectuer les observations avec des verres correcteurs.
Dans les lunettes à prismes l'écartement important des axes des objectifs augmente l'effet stéréoscopique.

Lunette de Galilée

L'objectif convergent donne d'un objet éloigné AB une image réelle inversée A'B' située très près de son plan focal image. L'oculaire divergent est placé entre l'objectif et cette image. Elle constitue pour l'oculaire un objet virtuel. L'oculaire donne de l'objet une image virtuelle A"B" dont le diamètre apparent θ" est supérieur au diamètre apparent θ de l'objet.
Pour ne pas accommoder un œil emmétrope vise à l'infini : le foyer image F'₁ de l'objectif est alors confondu avec le foyer objet F₂ de l'oculaire. La lunette est alors afocale. Pour observer sans fatigue un myope doit rapprocher l'oculaire de l'objectif alors qu'un hypermétrope doit l'éloigner.
Le grossissement est G = θ" / θ. Comme θ = A'B' / F'₁, on a G = F'₁. θ" / A'B' = F'₁.p₂ (p₂ est la puissance de l'oculaire).
Le grossissement est donc fonction des conditions d'observation. Dans le cas ou la lunette est afocale on a G = F '₁ / − f '₂.
Simple à construire la lunette de Galilée ayant un champ faible ne permet pas d'utiliser de forts grossissements ni de réticule mais sa clarté est supérieure à celle des autres lunettes.

 Télescopes.

Par rapport aux lunettes dioptriques les télescopes présentent un certain nombre d'avantages. Il n'y a pas d'aberrations chromatiques, certaines aberrations géométriques sont plus faciles à corriger, on peut utiliser des ouvertures bien supérieures à celles des lunettes enfin il est possible d'utiliser des dispositifs adaptatifs en découpant le miroir en un grand nombre d'éléments mobiles.
Les miroirs sphériques sont assez simples à réaliser, ils présentent une importante aberration sphérique. Il est possible de la corriger en combinant un miroir sphérique avec un ménisque (Maksutov) ou une lame de profil complexe mais réalisable assez facilement (lame de Schmidt). Avec ces corrections, il est possible d'obtenir des instruments à grand champ.

Les miroirs paraboliques sont rigoureusement stigmatiques pour un point à l'infini.
Par contre le miroir parabolique présente une aberration de coma très importante. On peut la limiter en combinant des miroirs concaves et convexes.
Montage Cassegrain
On utilise un miroir M₁ parabolique et un miroir M₂ hyperbolique dont le foyer F₁ est confondu avec le foyer FP de M₁.
Les rayons issus de l'infini convergent vers FP puis vers le foyer F₂ du miroir M₂. Le système est rigoureusement stigmatique pour les rayons parallèle à l'axe. Il faut par contre pratiquer une ouverture au sommet de M1 pour l'observation.
L'image primaire est virtuelle et pour les rayons peu inclinés sur l'axe, le miroir M2 donne un grandissement G = SF₂ / SF₁.
L'image finale est inversée.

Montage Gregorien
Si James Gregory a eu l'idée d'utiliser un miroir M1 parabolique et un miroir M₂ elliptique dont le foyer F1 est confondu avec le foyer FP de M₁ il n'avait pas les moyens techniques de le réaliser.
Les rayons issus de l'infini convergent vers FP puis vers le foyer F₂ du miroir M₂. Le système est rigoureusement stigmatique pour les rayons parallèle à l'axe. Ce montage exige également une ouverture au sommet de M₁ pour l'observation.
L'image primaire est réelle et pour les rayons peu inclinés sur l'axe, le miroir M₂ donne un grandissement G = SF₂ / SF₁.
L'image finale est droite. Cette propriété fait que cette monture a été très utilisée pour l'observation terrestre.