Le prisme
Un prisme est constitué par deux dioptres formant un dièdre. L'angle du dièdre A est l'angle du prisme. L'arête du dièdre est l'arête du prisme. En général le prisme est fermé par un plan opposé à l'arête qui constitue sa base. Un plan normal est un plan de section principale.
On suppose que le prisme est placé dans l'air, que son indice est N > 1 et que la lumière utilisée est monochromatique.
Déviation des rayons par un prisme
 |
On se place dans un plan de section principale. Un rayon incident arrive sur le dioptre d'entrée en J avec une incidence i1. Avec nos hypothèses, le rayon pénètre dans le prisme et se réfracte avec une émergence r1. Il arrive en K sur le dioptre de sortie avec une incidence r2.
|
Si r2 est inférieur à cet angle, il existe un rayon émergeant faisant l'angle i2 avec la normale au dioptre en K et contenu dans le plan de section principale.
Le rayon incident est dévié par le prisme d'un angle égal à D = (i1 − r1) + (i2 − r2).
La quadrilatère AKLJ ayant deux angles droits en K et J, on en déduit que A = r1 + r2.
On en déduit les relations suivantes :
Il n'y a un rayon émergeant que si r2 est inférieur à l'angle de réfraction limite. La somme r1 + r2 étant constante, il existe une valeur minimum im de i1 qui autorise la présence d'un rayon émergeant.
Minimum de déviation
Avec un goniomètre, on effectue le tracé point par point de la courbe de déviation D = f ( i1 ) pour un prisme d'indice N = 1,5 et d'angle A = 60 °.
Le point A correspond à l'incidence minimum im pour laquelle existe un rayon émergeant.
L'angle i2 vaut alors 90° .
Au point B (incidence rasante), l'angle i2 est égal à im.
Pour les points A et B, la déviation est maximum.
D'après le principe du retour inverse de la lumière, il existe deux valeurs de i1 (et donc de i2) qui donnent la même déviation.
Quand i1 = i2, la déviation est minimum.
En utilisant les formules du prisme, on peut retrouver cette propriété : La déviation est minimum si dD / di1 = 0.
- dD = di1 + di2
- dr1 + dr2 = 0
- cos i1.di1 = N.cos r1.dr1
- cos i2.di2 = N.cos r2.dr2
En éliminant dr1, dr2 = − dr1 et di2, il vient :
Cette expression s'annule si cos i1.cos r2 = cos i2.cos r1.
En élevant
au carré et en remplaçant cos² i par (1 − sin² i), on tire 
Comme N est supérieur à 1 le premier terme ne peut être nul. Il faut sin² i1 = sin² i2
Soit i2 = ± i1. La solution i2 = − i1 a été introduite par l'élévation au carré.
La déviation est minimum si i2 = i1 = i0 et donc r2 = r1 = r0. Le trajet du rayon est alors symétrique par rapport au plan médiateur du dièdre du prisme.
.
Mesure de l'indice d'un prisme
Soit Δ l'angle de déviation minimum.
On a Δ = 2.i0 − A → i0 = (A + Δ) / 2 or r0 = A / 2
On tire :
Si on mesure A et Δ avec un goniomètre de précision, il est possible de déterminer l'indice avec une incertitude de l'ordre de 10−5.
Stigmatisme du prisme
 |
On considère un prisme de petit angle A éclairé en incidence faible. Les rayons sur la figure sont tracés selon les lois de Descartes. On constate que le stigmatisme n'est approché que pour les rayons très peu inclinés. Sur la figure, le point vert est distant du point source S de d = OS.tan D ≈ OS.(N − 1).A |
Pouvoir dispersif du prisme
L'indice d'un milieu réfringent est fonction de la longueur d'onde λ de la lumière.
L'angle de déviation étant fonction de l'indice, est aussi fonction de λ. Examiner la figure ci-dessus dans le mode "dispersion".
Les valeurs de l'indice en fonction de la longueur d'onde utilisées sont :
N = 1,612 (0,768 µm) ; 1,623 (0,589 µm) ; 1,629 (0,540 µm) ; 1,635 (0,486 µm) ; 1,646 (0,434 µm).
Le pouvoir dispersif des prismes à été utilisé pour réaliser des spectroscopes et des spectrophotomètres. Il faut adapter la nature du milieu dispersif en fonction de la longueur d'onde de la lumière : les verres ordinaires sont opaques pour l'infra-rouge et l'ultra-violet. On a utilisé des prismes en NaCl, KBr et CsBr dans les spectroscopes à infra-rouge.
La possibilité de réaliser des copies de réseaux
très performants à un coût modique a rendu obsolète l'utilisation des prismes dans les systèmes monochromateurs.
Des prismes dispersifs ont une géométrie spéciale pour adapter la direction des rayons émergents. On trouve ainsi, les prismes à vision directe (déviation voisine de zéro) et les prismes d'Abbe ou de Pellin -Broca (déviation voisine de 90°)
Prismes redresseurs
Dans de nombreux systèmes optiques, il est nécessaire de modifier la direction des rayons lumineux. Les miroirs classiques présentent l'inconvénient d'introduire une lame à faces parallèles avant la surface réfléchissante et les miroirs métalliques sont fragiles. On utilise le plus souvent la réflexion totale sur des faces de prismes ou des faces de prisme métallisées.
Prisme d'Amici
C'est un prisme droit de section rectangle isocèle (45°, 90°, 45°) qui est utilisé comme redresseur
d'image. On éclaire le prisme normalement à une face non hypoténuse. Il y a réflexion totale sur la face hypoténuse et on récupère une image à 90° de la direction du faisceau objet.
Prisme de Dove
C'est aussi un prisme droit de section rectangle isocèle (45°, 90°, 45°) mais dont le sommet est tronqué. On éclaire le prisme parallèlement à sa base dont sous une incidence de 45°. Il y a réfraction sur la face d'entrée puis réflexion totale sur la face hypoténuse et réfraction sur la face de sortie. Le rayon émergent est parallèle au rayon incident.
Le système comportant une réflexion, l'image de sortie est
inversée. Le haut devient le bas ou la droite devient la gauche.

Prismes de Porro
Pour redresser l'image d'un objet donnée par un objectif, le système le plus simple est d'utiliser des prismes à réflexion totale.
Le véhicule de Porro est constitué de deux prismes droits dont la section est un rectangle isocèle et dont les arêtes sont perpendiculaires. Ils reçoivent la lumière sur leurs faces hypoténuses qui sont normales à l'axe optique du système. Comme les prismes sont attaqués sous une incidence très faible, les prismes n'introduisent pratiquement pas de dispersion. Si l'indice des prismes est supérieur à 1,41 alors il y a réflexion totale sur les faces non hypoténuses.
Chaque prisme est équivalent à deux miroirs orthogonaux.
Le premier prisme (rosé) dont l' arête est horizontale donne d'un objet une image dans laquelle haut et bas sont inversés.
Le second prisme (bleuté) dont l'arête est verticale donne de cette image une nouvelle image dans laquelle droite et gauche sont inversées.
Globalement, les deux prismes donnent une image totalement inversées de l'objet initial.
Les prismes de Porro sont surtout utilisé dans les jumelles car ils permettent le redressement indispensable de l'image.
Prismes de Schmidt-Pechan

Le prisme de Schmidt-Pechan est constitué par deux prismes. Il renvoie d'un objet une image totalement inversée.
Il remplit la même fonction que le prisme de Porro mais il n'introduit pas de translation de l'image ce qui permet d'obtenir des dispositifs plus compacts.
Le prisme supérieur est connu sous le nom de prisme de Schmidt et le prisme inférieur sous le nom de prisme de Pechan.
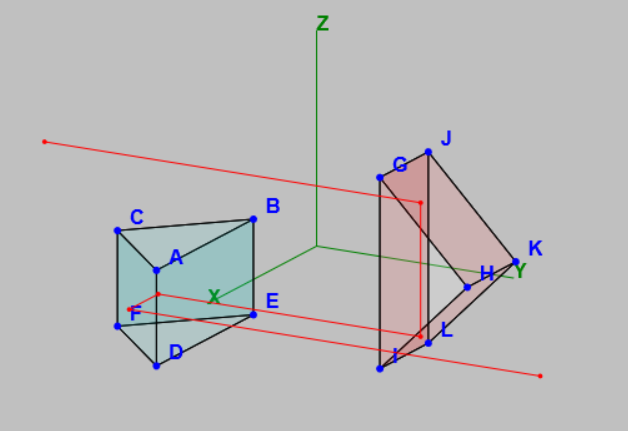
Géométrie des prismes :
Prisme d'entrée :
La face d'entrée (verticale) est la face ABFE. L'angle entre AD et AB est égal à 45° et l'angle entre AD et BC vaut 22,5°.
La face BCIF est aluminisée mais la face de sortie ADGE ne l'est pas.
Prisme de Schmidt :
La face d'entrée est parallèle à la face ADGE du premier prisme mais ces deux faces sont séparées par une lame d'air.
Par commodité ces deux faces sont représentées par une face unique dessinée en traits gras. L'angle entre EG et HJ vaut 67,5°. Les faces HJLK et HJNM du toit sont aluminisées.
Les normales à ces faces sont (−1, sin α, −cos α) et (−1, −sin α, cos α) avec α = 22,5°.
La face de sortie est NGDLJ.
Trajectoire d'un rayon :
On examine la cas d'un rayon incident qui arrive sur la face d'entrée sous incidence normale. Il rencontre la face AEGD avec une incidence de 45° : il y a réflexion totale. Sans la lame d'air qui sépare les deux prismes, le rayon incident traverserait cette face sans être dévié. Le rayon frappe ensuite la face BCIF aluminisée avec une incidence de 22,5°. Le rayon réfléchi arrive sur la face AEGD sous incidence normale et pénètre cette fois dans le second prisme.
Il y a réflexion sur la face NGDLJ (incidence 45°) puis sur les faces du toit (incidence 49,2°) puis sur AEGD (incidence 45°) . Finalement le rayon émerge parallèlement au rayon incident.
Un rayon horizontal ressort horizontal après six réflexions. On peut remarquer que les deux réflexions sur les faces du toit sont équivalentes à une réflexion sur un miroir vertical.
On trouve aussi les prismes d'Abbe-Koënig comparable au prisme de Schmidt-Pechan et le prisme en toit utilisé dans les appareils photographiques "reflex".
