Miroirs sphériques

Les miroirs sphériques sont des systèmes centrés simples dont l'étude montre l'intérêt et les limites de l'approximation de Gauss. Ce sont des systèmes de révolution et on conduit l'étude dans un plan contenant l'axe optique. Selon la première loi de Descartes un rayon incident contenu dans ce plan est réfléchi dans ce plan.

Miroir sphérique

Un miroir sphérique est une calotte sphérique réfléchissante. Le plan contenant l'axe optique et le rayon incident forment le plan d'incidence. Le rayon réfracté est contenu dans ce plan.

Stigmatisme du miroir sphérique

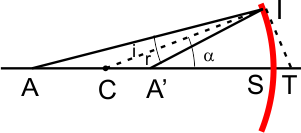Une source ponctuelle A émet un rayon ACS passant par le centre du miroir. Ce rayon arrive sous incidence nulle et se réfléchit sur lui-même. La normale au dioptre en I est CI. Un rayon AI arrive sur le miroir avec l'incidence i. La tangente au miroir en I est IT et le rayon du miroir CS = R Le rayon réfléchi est tel que r = − i. Ce rayon coupe l'axe optique en A'. Il y a stigmatisme si la position de A' est indépendante de la valeur de l'angle SCI = α

Les points A, C, A' et T forment une division harmonique car CI et IT sont les bissectrices de l'angle AIA'.
On a donc la relation 1 / CA + 1 / CA' = 2 / CT. (a)
Mais CT = R / cosα : La position de A' est fonction de α.
Pour un point quelconque de l'axe il n'y a pas stigmatisme.
Le centre du miroir et sa surface sont à eux-mêmes leur propre image sont stigmatiques.

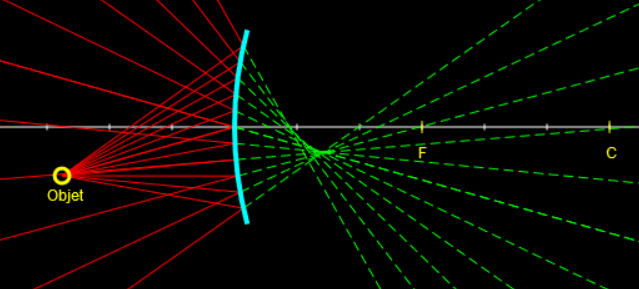
Illustration du non stigmatisme d'un miroir sphérique.

Relations de conjugaison

Toutes les figures illustrant ce paragraphe figurent dans le programme ci-dessous.

Si on se place dans les conditions de Gauss on peut confondre le cosinus α de la relation (a) avec 1.
Les points A, A', C et S forment également une division harmonique et on obtient la relation de conjugaison :

Cas particuliers
Si SA = R alors SA' = R : le centre est sa propre image.
Si SA = ∞ alors SA' = R / 2 = f. Le foyer d'un miroir (image d'un point à l'infini) est situé au milieu de CS.

Si le miroir est concave, le foyer est réel. Il est virtuel pour un miroir convexe.

Cette relation est également valable pour des points proches de l'axe avec des rayons peu inclinés sur l'axe optique.
Dans l'approximation de Gauss, un miroir de faible ouverture donne d'un objet plan normal à l'axe optique une image plane normale à l'axe. On définit les plans objet, image et focal qui sont les plans normaux à l'axe optique qui contiennent l'objet, l'image et le foyer du miroir.

Construction géométrique des images

Plan objet à l'infini.
L'image d'un point A situé sur l'axe à l'infini est le foyer F. Pour un point B situé à l'infini en dehors de l'axe et dont la distance angulaire avec A est α a son image au point B' situé à l'intersection du plan focal et la droite BC inclinée de l'angle α sur l'axe optique. Comme α est petit, on a : A'B' = − f.α.

Plan objet dans le plan focal.
L'image est située à l'infini. L'image d'un point B en dehors de l'axe est à l'infini dans la direction BC. Le diamètre apparent de l'image est α = AB / − f.

Plan objet quelconque.
Pour déterminer la position de l'image, on peut utilise la construction suivante : A partir d'un point de l'objet, on trace un rayon qui passe par le centre optique et un rayon parallèle à l'axe optique. Le premier se réfléchit symétriquement à l'axe optique et le second après réflexion passe par le foyer du miroir. L'intersection (réelle ou virtuelle) des deux rayons donne le point image correspondant.
On peut également utiliser un rayon passant par le centre C et qui se réfléchit sur lui-même pour effectuer la construction de l'image..

Grandissement linéaire

Le grandissement linéaire est le quotient γ = A'B' / AB
Si ce rapport est positif, l'image est droite sinon elle est inversée.
De la similitude des triangles ABS et A'B'S on tire γ =A'B' / AB = − SA' SA
Comme le rayon BC passe par B', on a aussi γ = CA' / CA : l'image est homothétique de l'objet par rapport au centre du miroir.

Le programme ci-dessous permet d'examiner tous les cas de figures (objet réel, virtuel et à l'infini) pour des miroirs convexes ou concaves. Utiliser la souris pour glisser l'objet.

Formules de Newton

Il est possible d'utiliser le foyer comme origine pour établir les relations de conjugaison. La distance focale est SF = f .

On effectue une construction graphique de l'image. Dans les conditions de Gauss, il est possible de confondre les arcs SI et SJ avec les normales en S à l'axe optique. La similitude des triangles A'B'F et SIF donne A'B' / SI = FA' / FS et aussi A'B' / AB = FA' / FS . γ = − FA' / f La similitude des triangles ABF et SJF donne SJ / AB = FS / FA et aussi A'B' / AB = FS / FA . γ = − f / FA

On en déduit les formules de Newton γ = − FA' / f = − f / FA et FA.FA' = f ².

Les formules de Newton avec origine au foyer sont bien sûr équivalente aux formules de conjugaison avec origine au sommet. On utilisera comme origine S ou F le point le plus important dans le problème étudié.

Usages

Les miroirs sphériques sont utilisés dans les télescopes comme miroirs primaires ou secondaires.

A surface égale le champ d'un miroir convexe est plus grand que celui d'un miroir plan. Un miroir convexe donne d'un objet réel une image réelle, droite et plus petite que l'objet : On les utilise comme rétroviseurs, miroirs de sécurité.

On utilise des miroirs concaves comme miroir de rasage ou de maquillage.